日本応用数理学会
2021年 研究部会連合発表会
プログラム
2021年2月24日
ご注意：本プログラムは暫定版であり変更される可能性があります．
＜各種会合＞
- 3月4日 12:45 — 13:10 「JSIAM Letters編集委員会」
- 3月5日 12:30 — 13:30 「キャリアデザインのためのランチミーティング」
- 3月5日 16:30 — 17:30「研究部会連絡会」
＜講演＞
3月4日
3月5日
▷ 行列・固有値問題の解法とその応用(1) ［3月4日：09:40-11:00：A］（座長：廣田 悠輔（福井大学））
- フィルタ対角化法に用いる初期ベクトルの組に改良を加える試み / ○村上 弘 (東京都立大学) [概要]
フィルタ対角化法を用いて，実対称定値一般固有値問題の固有対でその固有値が指定された区間にあるものを一斉に近似して求める．その際に，フィルタに適用する最初のベクトルの組として各成分が一様乱数から生成されたものをそのまま用いるのではなくて，あらかじめ適切な処理を加えて求めたい固有ベクトルの割合を高めたものを用いる．そのことにより近似固有対の精度を向上させることを試みる．
- 二等分点以外を分割点に用いる帯行列分割統治法の計算量評価 / ○廣田 悠輔 (福井大学) [概要]
実対称帯行列の固有値問題に対する分割統治法では，二等分点以外の点を適切に選んで行列を再帰分割すると，二等分点のみを用いた場合に比べて解法の計算量を削減できる．特にデフレーションが生じない仮定のもとでは，計算量を厳密最小化する分割点が動的計画法により現実的な時間で求められる．本発表では，デフレーションが生じない仮定のもとで計算量を最小化および準最小化するように選ばれた分割点を，デフレーションが生じる現実的な状況下の分割統治法で用いた場合の計算量の評価結果について報告する．
- Brauerの定理を利用した正方行列のスペクトル半径の上限に対する数値計算法 / ○伊五澤 彩乃 (岩手大学), 宮島 信也 (岩手大学) [概要]
複素正方行列Aのスペクトル半径の上限を数値的に求める方法を提案する. この方法はBrauerの定理と精度保証付き数値計算を利用したものであり, Aが非Hermite行列の場合でも適用可能である. 数値実験により, 多くの場合において, 提案する方法はAのすべての固有値に対する精度保証付き数値計算を単純に応用した方法よりもタイトな上限を与えることを示す.
- 四元数行列のすべての標準固有値に対する 精度保証付き数値計算 / ○丹野 遼太郎 (岩手大学), 宮島 信也 (岩手大学) [概要]
四元数を成分にもつn次正方行列の右固有値は一般に無限個存在する. それらの中には常に, 虚部が非負の複素数であるものが重複を込めてちょうどn個存在する. これらn個の右固有値は標準固有値と呼ばれる. 本講演では, すべての標準固有値を包含するn個の複素区間（複素平面上の円盤）を数値的に算出する方法を提案する. また, 数値実験により, 提案した方法の有効性を示す.
▷ 位相的データ解析 (1) ［3月4日：09:40-11:00：B］（座長：大林 一平（理化学研究所、京都大学））
- The Whole in the Parts: Putting nD Persistence Modules Inside Indecomposable (n+1)D Ones / Buchet Mickaël (Institute for Geometry, Graz University of Technology), ○Escolar Emerson Gaw (神戸大学大学院人間発達環境学研究科) [概要]
位相的データ解析において、マルチパラメータ付きデータのパーシステンスを調べるために、多次元パーシステンスが提案された。本講演では、多次元パーシステンス加群が、次元が１つ上の直既約パーシステンス加群に含まれる現象を調べて、多次元パーシステンスの代数的な複雑さをこの観点から示す。本講演はプレプリント https://arxiv.org/abs/2012.02467 にもとづく。
- A correspondence between Schubert cells and persistence diagrams / ○許 晨光 (京都大学大学院理学研究科数学・数理解析専攻), 平岡 裕章 (京都大学高等研究院) [概要]
Topological data analysis (TDA) is an arising new field studying the geometry and topology of data using mainly algebraic topology approaches. As a pivotal tool of TDA, persistent homology provides a universal method for capturing the topological properties of filtered spaces derived from real-world data. It has found applications in a wide range of subjects as diversified as cosmology, medical imaging, botany, and material science.
While there are already different effective ways to study persistent homology, we take an algebro-geometric perspective to approach it in this research via observing the high similarity between partial flags and persistence modules. We prove a bijective correspondence between persistence diagrams and Schubert cells of an associated partial flag variety. This correspondence provides a passage for transferring the partial order structure and the multiplicative structure from partial flag varieties to persistence modules. It also opens a door for exploring further possibilities of adding more structures on persistence modules.
- 区間表現による2Dパーシステント表現の近似 / 浅芝 秀人 (静岡大学), Emerson Escolar (神戸大学), ○中島 健 (理研AIP), 吉脇 理雄 (理研AIP) [概要]
位相的データ解析で使われるパーシステント図（PD）は、多元環の表現論の立場から見るとA_n型クイバーの表現（1Dパーシステント表現）の直既約分解を提示したものになっています。この視点はPDの高次化を可能にしますが「無限表現型多元環上の加群の直既約分解」という難題を伴います。本講演では、与えられた2Dパーシステント表現を「区間表現」という扱いやすい直既約表現の “直和” として近似するメソッドを提示します。
- パーシステントホモロジーと機械学習を用いたガラス形成における局所構造変化の抽出 / ○平田 秋彦 (早大), 和田 智秀 (東北大), 大林 一平 (理研／京大), 平岡 裕章 (京大) [概要]
物質を液体状態から冷却した際に多くの場合結晶化が起こるが、液体に類似した構造を持ち越しガラス状態となる場合がある。一般にガラス化の際、原子のダイナミクスは大きな変化を起こすが、静的な構造の変化は少ないと言われている。本研究では、パーシステントホモロジーと機械学習を組み合わせることにより、液体→ガラスの構造変化に特に関係した局所構造をガラス構造から抽出することを試みた。結果は講演にて報告する。
▷ 応用カオス(1)・乱数の生成と評価セッション ［3月4日：09:40-11:00：C］（座長：山口 明宏（福岡工業大学））
- 乱数の統計検定に関する考察 / ○奥富 秀俊 (東芝情報システム株式会社) [概要]
系列が乱数とみなせるか否かを推測統計学の検定を利用して判定する手段を乱数検定とよぶ．本発表では，乱数検定を推測統計学の基本に立ち返り，母集団と標本の関係にもどって再考察する．考察では，乱数検定は母集団を厳密に既知かつ真として扱えることから，標本の無作為抽出性を評価したことになる（統計検定は標本の無作為抽出性を大前提とするため評価対象ではない）等の特殊性について触れる．
- 量子乱数生成による量子コンピュータの安定性解析 / ○田村 賢太郎 (慶應義塾大学大学院理工学研究科), 鹿野 豊 (慶應義塾大学量子コンピューティングセンター・JSTさきがけ・チャップマン大学量子科学研究所), レイモンド ルディー (IBM東京基礎研究所・慶應義塾大学量子コンピューティングセンター) [概要]
量子コンピュータの出力が信頼できるものであるかはデバイスの状態に依存するため, デバイスの状態を解析することには価値がある. ただし, デバイスの状態が時事刻々変化するものであった場合, その解析結果は一時的にしか意味を持たない. デバイスの状態の解析結果が継続的に意味を持つためには, デバイスの状態が安定していることが不可欠である. 量子コンピュータでは入力とプログラムによって出力の確率分布が決まるため, デバイスの安定性は出力の確率分布の同分布性として反映される. 本研究では量子ビットで生成した乱数列の同分布性を調べることで, 量子コンピュータの安定性を解析する手法を提案する.
- Bernoulli写像のカオス真軌道を用いた擬似乱数生成法のNewton法による高速化 / ○山口 明宏 (福岡工業大学), 斉藤 朝輝 (公立はこだて未来大学) [概要]
著者等は，これまでに代数的整数を用いてBernoulli写像のカオス真軌道を計算して擬似乱数を生成する方法を提案し，NIST SP800-22 や TestU01で良好な結果が得られることを報告している．しかし，カオス真軌道の計算に多くの計算時間を要するためその高速化が課題の一つであった．本研究では，Bernoulli写像のカオス真軌道から生成する2値系列をNewton法を用いて直接計算することで，カオス真軌道による擬似乱数と同等の擬似乱数を高速に生成する方法を提案し，真軌道計算による方法とNewton法による方法との計算量の比較，Newton法で生成した擬似乱数と真軌道計算による擬似乱数について一致しないビットが生じる確率を解析した結果を報告する．
- 整数上のロジスティック写像による擬似乱数生成器における部分系列カオス尺度を用いた乱数性の改善法 / ○宮﨑 武 (北九州市立大学), 荒木 俊輔 (九州工業大学), 上原 聡 (北九州市立大学), 野上 保之 (岡山大学) [概要]
本稿は，整数上のロジスティック写像による擬似乱数生成において，生成パラメータを更新した際に短い周期をもつループに到達する確率が数%存在することを示す．また，短いループに到達する前の準ループ状態が乱数性に与える影響を示す．この影響を取り除くため，末尾の部分系列におけるカオス尺度を用いた準ループ状態判定法を提案し，実際に得られた擬似乱数の統計的性質が改善することを数値実験によって示す．
▷ 連続体力学の数理(1) ［3月4日：09:40-11:00：D］（座長：新納 和樹（京都大学））
- Atomistic-to-continuum limits of planar disclinations / ○Cesana Pierluigi (Kyushu University), van Meurs Patrick (Kanazawa University) [概要]
We describe rotational mismatches on the triangular lattice as the minimizers of a functional accounting for nearest-neighbor interactions. We are interested in the asymptotics of the energy minima and minimizers as the lattice spacing vanishes which we compute exactly with Gamma-convergence. We perform some numerical calculations for the discrete model and show that both the shape of the solutions as well as the values of the energies are in agreement with classical results for positive and negative disclinations.
- 陸への遡上を考慮した津波の解析について / ○舘山 正佳 (明治大学理工学研究科数学専攻), 矢崎 成俊 (明治大学) [概要]
津波の陸への遡上は甚大な被害をもたらす．
本講演では，被害を大きくしている要因を，３段階の変化を持つ海底の上で浅水波方程式を解くことによって調べ，
次の三点について発表する．
(1) 津波が陸地を遡上するときの数値計算手法の考案，
(2) 数値計算データから津波の波長，遡上距離，時間，海底の深さの相互関係の評価，
(3) 波長の大きさ，海底の勾配，後続の波が第一波よりも高くなるといった性質の考察．
- Maxwell 方程式に対する選点法を用いた isogeometric 境界積分法における Calderón の前処理について / ○田原 寛太 (京都大学情報学研究科), 新納 和樹 (京都大学情報学研究科) [概要]
Maxwell 方程式に対する選点法を用いた isogeometric 境界積分法における Calderón の前処理について発表する. 一般に Calderón の前処理を EFIE に用いる場合, 離散化の際に双対基底が必要なことが知られているが isogeometric 境界要素法では双対基底を簡単に構成できることを示す.
- 非局所性を有するBiot層状材料における波動の反射・透過 / ○廣瀬 壮一 (東京工業大学), Zhang Qingxuan (東京工業大学), Tomar Sushil Kumar (Panjab University), Singh Dilbag (Panjab University) [概要]
本研究では，非局所性を有するBiot材料からなる層構造における波動の反射・透過問題を解析した．まず，応力成分に積分型の非局所性を仮定してBiotの運動方程式並びに境界条件を導き，定常状態における変位ポテンシャルを運動方程式と境界条件に代入することによって，非局所性を有するBiot材料における波動の位相速度と反射・透過係数を求めた．層厚，入射角，周波数，非局所パラメータなどが反射・透過係数に及ぼす影響を考察した．
▷ 離散システム(1) ［3月4日：09:40-11:00：E］（座長：澤 正憲（神戸大学））
- Balanced AND-OR木上の最適な乱択アルゴリズム / ○伊藤 風輝 (東京都立大学) [概要]
AND-OR木とは、各レイヤーにANDノードとORノードが交互に現れ、葉ノードがブール変数となっている木である。AND-OR木は各変数が一度しか現れないブール関数と解釈でき、いわゆるクエリー計算量が興味の対象となる。この計算量は根の値を求める過程で質問された変数の個数である。乱択アルゴリズム（いわゆるラスベガス法）を考え、ゲーム論的な均衡値や、均衡点の一意性が研究されている。本発表では木の転置という概念を用いて、balanced AND-OR木（対称的な木）に対する最適な乱択アルゴリズムが非一意的であることを示す。
- 完全マッチング遷移問題に関する計算量下界について / ○馬場 康輔 (九州大学), 来嶋 秀治 (九州大学), 山口 勇太郎 (九州大学) [概要]
組合せ問題に対して，実行可能解に隣接関係を導入して得られるグラフを解空間グラフと呼ぶ．組合せ遷移問題とは，与えられた2つの実行可能解について，それらを結ぶ，解空間グラフ上の経路が存在するか否かを判定する問題である．本発表では，グラフの完全マッチングの遷移問題に対して，制限された計算モデルにおける時間計算量の下界を議論する．
- あるRIP行列とErdo”s-Falconer型の距離問題 / ○佐竹 翔平 (熊本大学) [概要]
制限等長性 (RIP)を保証する行列のdeterministicな構成は圧縮センシング理論における１つの重要なテーマであり,
これまで組合せ論や整数論との関連を深めながら盛んに研究がなされてきました.
一方, 有限体上のErdo”s-Falconer型の距離問題はBourgain-Katz-Tao (2004)によって提案され,
sum-product estimateやある種の「距離グラフ」のエクスパンダ―性などに密接に関連します.
本講演では, ある特定の行列の制限等長性から, Erdo”s-Falconer型の距離問題に対する1つの解が導かれることを示します.
- 非線形状態空間システム解析における代数的マトロイドの応用について / ○小松 瑞果 (神戸大学大学院システム情報学研究科), 谷口 隆晴 (神戸大学大学院システム情報学研究科) [概要]
システムバイオロジーなどの分野では，多項式で表された非線形の状態空間モデルがよく用いられる．そのようなモデルは素イデアルを定めることが多く，それに対応する代数的マトロイドを考えることができる．本発表では，状態空間モデルからそのように誘導された代数的マトロイドのシステム解析への応用について述べる．
▷ 行列・固有値問題の解法とその応用(2) ［3月4日：11:10-12:30：A］（座長：相島 健助（法政大学））
- 特異対称系に対するGMRES法とRRGMRES法の数値実験と収束解析 / ○杉原 光太 (国立情報学研究所), 速水 謙 (国立情報学研究所 総合研究大学院大学) [概要]
電磁場解析等で生じる特異対称系において，右辺が係数行列の値域に属さない場合，丸め誤差に強いGMRES法とRange Restricted GMRES (RRGMRES)法の収束性を，数値実験ならびに理論から比較する．
両手法の破綻ならびに収束に関する理論を使い，GMRES法が理論と異なり，数値実験では収束不十分な時がある原因を報告する．またRRGMRES法の像空間成分が正則系へのGMRES法と等価であることを示し，その収束性を理論ならびに数値実験から解析する．
- Behaviour of GMRES and block GMRES for matrices with multiple and clustered eigenvalues / ○LIAO Zeyu (The Graduate University for Advanced Studies, SOKENDAI), HAYAMI Ken (National Institute of Informatics and The Graduate University for Advanced Studies, SOKENDAI) [概要]
We will study the numerical behaviour of GMRES and block GMRES for coefficient matrices with multiple and clustered eigenvalues and try to analyze it.
- GMRES(m)法における行列データの低精度化に関する検討 / ○深谷 猛 (北海道大学，JST さきがけ), 岩下 武史 (北海道大学) [概要]
近年，単精度や半精度に代表される，低精度演算・データを積極的に利用した数値計算アルゴリズムの研究開発が活発に行われている。本発表では，疎行列を係数とする連立一次方定式の代表的解法である，リスタート付きGMRES法（GMRES(m)法）のArnoldi過程で用いる係数行列データの低精度化を試みる。様々なテスト行列を用いて，実験的に収束性を調査し，低精度化の可能性を探る。
- デコンボリューション問題におけるcondition L-curveの検討 / ○久保井 五貴 (福井大学), 田中 利佳 (福井大学), 小澤 伸也 (福井大学), 細田 陽介 (福井大学), 高田 雅美 (奈良女子大学), 木村 欣司 (福井大学) [概要]
本研究では 2 次元ボケ画像のデコンボリューション問題を設定し，線形反復解法によるボケ画像鮮明化に取組んだ．今回は，対象画像にノイズ有りの問題設定を設け， LSMR法及びLSQR法によるデコンボリューションを行った．その際に，停止条件としてcondition L-curveを採用する．復元度の基準として相対誤差や PSNRを利用し，ノイズ有り画像鮮明化問題に対するLSMR法及びLSQR法の数値特性を評価する．
▷ 位相的データ解析 (2) ［3月4日：11:10-12:30：B］（座長：井元 佑介（京都大学））
- アトラクターのトポロジーに着目した因果推定手法について / ○板東 弘晃 (京都大学情報学研究科システム科学専攻), 鍛冶 静雄 (九州大学マス・フォア・インダストリ研究所), 谷口 隆晴 (神戸大学システム情報学研究科計算科学専攻) [概要]
相関システムは脳科学, 個体群生態学など広く存在する. そして, 二つの相関システムの間の因果関係を検出することは困難かつ重要である. 本研究では, 結合ダイナミカルシステムから測定した時系列データを用いて因果推定するため, 遅延埋め込みとパーシステントホモロジーを組み合わせた新しい手法を提案する.
- 画像の色数に着目した重み付きグラフの構成, 及びVietoris-Rips複体を用いた主対象検出への応用 / 長瀬 准平 (芝浦工業大学大学院理工学研究科), 高木 志郎 (東京大学大学院新領域創成科学研究科), 坂本 龍太郎 (慶応大学理工学部数理科学科), ○浅尾 泰彦 (理研AIP) [概要]
与えられた画像内の主要な被写体を検出する処理（主対象検出）は, これまで多くの手法が提案・実装されており, AI技術が近年急速に発展し実生活に普及している中では欠かせないものとなっている. 本研究では, 画像の局所的な情報たちの関係を記述した重み付きグラフに対して, Vietoris-Rips複体と呼ばれる単体複体を構成することで, 画像全体の情報が局所的にどこまで縮約されるかを調べる手法を提案する. ただし情報が縮約しているというのは, 画像の部分領域Dに対して, D内で使用している色の数とDの面積の比が相対的に大きいことを指す. このことを領域Dの情報濃度が高いと表現することにする. 本研究では情報濃度の高い領域を複体の極大単体を調べることで検出し, それらをいくつか重ねて表示することで主対象検出を試みた.
- レーブ順序法の画像輪郭抽出への応用 / ○宇田 智紀 (東北大学材料科学高等研究所), 中野 直人 (京都大学国際高等教育院附属データ科学イノベーション教育研究センター), 池 祐一 (富士通研究所人工知能研究所) [概要]
画像輪郭抽出では画素値の微分相当量が本質的な役割を持つものが多く，ノイズ画像からの輪郭抽出は一般には難しいことが知られている．レーブ順序法は，グリッド上のスカラーデータ（例えばグレースケール画像）からそのレーブグラフを計算する位相的データ解析手法で，ノイズに強い性質を持つ．本講演では，レーブ順序法の入力グリッドに工夫を加えることで強ノイズ画像の輪郭抽出を堅牢に実現できることをご報告する．
▷ 応用カオス(2) ［3月4日：11:10-12:30：C］（座長：井上 啓（山口東京理科大学））
- ３自由度結合カオス系の解析－同期、クラスタリング、発散現象とその条件－ / ○加納 拓実 (京都大学工学部情報学科数理工学コース), 梅野 健 (京都大学) [概要]
3つの同じカオス系に対して相互に作用するような結合をし、その軌道の振る舞いを観察したところ、基本的に3つの系の軌道は独立していたが、ある条件下では軌道が正または負に発散する発散現象や、初期値によらず3つの系が同じカオス軌道をとる同期現象、3つのうち2つの系が同期し、もう一つの系は独立な軌道を取るクラスタリングが見られた。またそれらの条件がシミュレーションや数学的な理論を用いた解析により得られた。
- 拡張SGB変換の臨界指数について / ○大久保 健一 (大阪大学), 梅野 健 (京都大学) [概要]
講演者は, 超一般化Boole変換(SGB)変換について冪指数βを用いたさらなる拡張を行ってきた. 今までの講演では, 拡張したSGB変換があるパラメータの範囲の時, エルゴード特性の一部であるexact性を持つことを発表した. 本講演では, パラメータKが偶数の場合に, パラメータαを0に近づけた場合の臨界指数が1/2となることを示す.
- 普遍ブッキングカーブに基づく汎用ダイナミックプライシングアルゴリズム / ○新谷 健 (京都大学大学院情報学研究科), 梅野 健 (京都大学大学院情報学研究科) [概要]
予約を伴うサービス商品のブッキングカーブは、実績データの解析から与えられる商品固有のパラメータを用いた指数関数群で表すことができる。
その性質を利用し、本研究では「相対価格弾力性」という考え方を提唱した上で、それらを統合した汎用的なダイナミックプライシングアルゴリズムを提案する。
- Umklapp過程の無い非線形格子モデルの構成と熱伝導特性 / ○吉村 和之 (鳥取大学), 土井 祐介 (大阪大学), 北村 智哉 (鳥取大学) [概要]
固体のフォノン熱伝導に関して、熱抵抗はUmklapp過程と呼ばれるフォノン相互作用によってのみ生じ、正常過程と呼ばれる相互作用は熱抵抗に寄与しないという仮説が、パイエルスによって提唱され信じられている。しかしながら、これまで適切な格子モデルが無かった為、格子力学に基づいた仮説の検証はなされていない。我々は、Umklapp過程が無く正常過程のみを含む特殊な１次元非線形格子モデルを構成した。この格子モデルを用いて非平衡分子動力学による熱伝導シミュレーションを行い、Umklapp過程が無い場合に熱抵抗がゼロになることを示した。すなわち、パイエルスの仮説が正しいことの直接検証に成功した。
▷ 連続体力学の数理(2) ［3月4日：11:10-12:30：D］（座長：木村 正人（金沢大学））
- 狭空間に閉じ込められた弾性膜の座屈を伴う破壊 / ○増田 千紘 (横国環情), 工藤 大嗣 (横国環情), 松井 和己 (横国環情), 田中 良巳 (横国環情) [概要]
弾性シートの座屈を伴うき裂伸展挙動，とくに系を平行な2枚の剛体板の間の空間に閉じ込めて面外変形の大きさを拘束した場合の挙動を実験的に調べ，その結果をスケーリング解析をした．さらに，有限要素法による変形パターンの再現を行った結果についても報告する予定である．
- 動的自己相似亀裂を表現する特異積分方程式の変数変換について / ○平野 史朗 (立命館大学), 伊藤 弘道 (東京理科大学) [概要]
自己相似、かつ動的に破壊する直線亀裂の面外問題を考察する。この問題では2次元波動方程式から出発するが、自己相似性を活かした変数変換により変数を1つ減らし、楕円形の方程式に帰着させることが可能である。従来は等角写像を用いる方法が提案されていたが、それとは異なる方法により特異積分方程式に帰着させ解を得た。更に亀裂端近傍の応力を正則化しエネルギー解放率を数値的に求めることに成功した。
- 多孔質媒質中におけるk-epsilonモデルに現れる初期条件鋭敏性とその数理的応用 / ○鈴木 岳人 (青学大理工) [概要]
これまでの著者の研究では、多孔質媒質中の乱流にk-epsilonモデルを適用し、特に渦粘性が初期値に特異な鋭敏性を持つことを示してきた。ここではその鋭敏性の数理的応用、特にneural networkへの応用を考える。いくつかの仮定の下、その鋭敏性を特徴づける関数の解析的表現を見出すことができた。
- フェーズフィールド法による水圧破砕進展モデル / ○吉岡 慶太 (Helmholtz Centre for Environmental Research) [概要]
亀裂進展におけるフェーズフィールド法の応用は90年代半ばに始まって以来、近年では最も標準的ともいえる手法とまで発展を遂げてきている。亀裂進展モデルに応用された際の大きな利点の一つは、場当たり的な破壊基準や亀裂進展方向への制限を必要とせずに、２次元および３次元の複雑な未決定の亀裂の経路を捉えられることにある。
この講演では、FrancfortとMarigoの破壊に対する変分法の正則化として提案されたフェーズフィールド法を簡単に紹介し、水圧破砕への応用を考察する。並びにフェーズフィールド法では、陽的に求められない応力拡大係数や亀裂開口幅の復元について解析解との比較を行う。
さらに複数の亀裂が同時に進展する問題を変分法におけるエネルギー最小化問題として考察する。この際に、亀裂の対称性の喪失するケースが常により多くのエネルギーを解放することを、安定性解析およびフェーズフィールド法を用いた数値計算において示す。
▷ 離散システム(2) ［3月4日：11:10-12:30：E］（座長：谷川 眞一（東京大学））
- 付値マトロイドのランク関数と閉包関数について / ○大中 亮磨 (東京大学) [概要]
付値マトロイドはマトロイドの一般化にあたる概念であり，マトロイドの基族上の関数で交換公理を満たすものとして定義される．マトロイドと本質的に等価な公理系が多数存在するように，付値マトロイドにも等価な公理系を考えることができる．本発表では整数値付値マトロイドの等価な公理系として，マトロイドのランク関数と閉包関数の一般化にあたる関数クラスを紹介する．
- 離散協力ゲームにおける平等主義的解の性質 / ○大塚 貴郁 (東京工業大学工学院経営工学系修士課程1年) [概要]
本研究は，特性関数値が整数値であり，利得ベクトルが整数ベクトルである協力ゲームにおける平等主義的解(egalitarian solution)の性質について分析する．平等主義的解とは，協力ゲーム理論における解概念の一つであり，実数値の協力ゲームにおいて良い性質をもつことが知られている．本研究は，実数の場合に平等主義的解に対して成り立つ良い性質が，整数値のゲームでは成り立たないことを示す．さらに，平等主義的解の変種であるローレンツ安定集合という解概念に着目し，Frank–室田による，Ｍ凸集合上の辞書的最適基に関する離散凸解析の結果を利用することにより，整数値をもつゲームにおいて，解概念としてのローレンツ安定集合が良い性質をもつことを明らかにする．
- Existence of EFX for Two Additive Valuations / ○馬原 凌河 (京都大学) [概要]
Fair division of indivisible items is a well-studied topic in Economics and Computer Science.
The objective is to allocate items to agents in a fair manner, where each agent has a valuation for each subset of items.
Envy-freeness is one of the most widely studied notions of fairness. Since envy-free allocations do not always exist when items are indivisible, several relaxations have been considered. Among them, possibly the most compelling one is envy-freeness up to any item (EFX), where no agent envies another agent after the removal of any single item from the other agent’s bundle. However, despite significant efforts by many researchers for several years, it is known that an EFX allocation always exists only in limited cases.
In this talk, we introduce our results that an EFX allocation always exists when each agent is of one of two given types, where agents of the same type have identical additive valuations.
This is the first such existence result for non-identical valuations when there are any number of agents and items and no limit on the number of distinct values an agent can have for individual items.
- マトロイドランク効用関数をもつ組合せ市場の価格付け / Bérczi Kristóf (Eötvös Loránd University), ○垣村 尚徳 (慶應義塾大学), 小林 佑輔 (京都大学) [概要]
この講演では，組合せ市場において，価格付けによって社会的効用を最大化する問題を扱う．ここでは価格付けとして，買い手が動的に市場にやってくる状況においても最大の社会的効用を得られるものを考える．本講演では，買い手の効用関数がマトロイドのランク関数で与えられる2人市場において，マトロイドが以下のいずれかを満たす場合に価格付けを得るための多項式時間アルゴリズムを与えた：（１）１つのマトロイドが単純な分割マトロイドである場合（２）マトロイドがstrongly base orderableマトロイドである場合．
▷ 行列・固有値問題の解法とその応用(3) ［3月4日：13:30-14:50：A］（座長：速水 謙（国立情報学研究所））
- Deflation を用いた幾つかの非対称行列用クリロフ部分空間法の性能比較 / ○高谷 周平 (個人) [概要]
正定値対称行列用の解法であるdeflated CG法には初期の研究において複数の流儀があり、Vuikらはそれらを4つに分類した。これら4つのdeflationの技法をCG法以外のクリロフ部分空間法へ適用した線形代数ソルバの開発を筆者は続けている。本講演では、CRS法を含む非対称行列のためのクリロフ部分空間法の幾つかにdeflationの技法を適用して得られた解法と、これらの解法の性能を大規模並列有限要素接触解析問題で比較した結果について報告する。
- 3次元モデル再構成問題に現れる鞍点型連立一次方程式に対する前処理付き反復法の性能評価 / ○石川 翔大 (筑波大学), 多田野 寛人 (筑波大学), 齋藤 歩 (山形大学) [概要]
3次元物体の連続した断層画像からボリューメトリックモデルと呼ばれる3Dモデルを構成する手法の一つに，鞍点型連立一次方程式の求解を必要とするアプリケーションが存在する．
我々は，鞍点型連立一次方程式のブロック構造を利用して，求解しやすい方程式へ変形することで，高速な求解手法を提案した．
本発表では，同法の内部で現れる複数右辺ベクトルを持つ連立一次方程式に対する前処理付き反復法の性能評価を行う．
- Sylvester方程式に対するglobal Krylov部分空間法のresidual gap評価とその改善 / ○相原 研輔 (東京都市大学), 今倉 暁 (筑波大学), 保國 惠一 (筑波大学) [概要]
Sylvester方程式に対して短い漸化式を用いるKrylov部分空間法の数値的な収束性について議論する．具体的には，global BiCGSTAB法やglobal CGS2法で生じるresidual gap（真の残差と漸化式から求まる残差との差）について解析し，反復中の残差ノルムの最大値が初期残差ノルムに比べて相対的に大きいとき，近似解精度が劣化することを示す．また，近似解精度を改善するため，最近提案された相互作用型残差スムージングを適用し，丸め誤差解析と数値実験によりその有効性を示す．
- 複数右辺ベクトルを持つ線形方程式に対するblock generalized CGS法 / ○今倉 暁 (筑波大学), 相原 研輔 (東京都市大学), 保國 惠一 (筑波大学) [概要]
複数右辺ベクトルを持つ線形方程式に対する有力な解法として知られるblock Krylov部分空間法は、通常のKrylov部分空間よりも広いblock Krylov部分空間を利用して収束性を改善する拡張・改良法である。これまでに様々なKrylov部分空間法のblock版への拡張が提案されているが、CGS系統の解法については、block版への拡張が困難であり、導出されていなかった。本研究では、CGS法の一般化であるgeneralized CGS（GCGS）法に着目し、そのblock版への拡張であるblock GCGS法を導出する。
▷ 計算の品質 (1) ［3月4日：13:30-14:50：B］（座長：渡部 善隆（九州大学））
- 強制遅延Duffing方程式の逆分岐図問題と精度保証 / ○大石 進一 (早稲田大学), 関根 晃太 (東洋大学) [概要]
強制項のある遅延Duffing方程式の分岐図を数値積分法によって計算し，その分岐図を構成する分数調波解などを精度保証付き数値計算によって存在証明する問題を取り扱う．このような分岐図に現れている解を再構成（その存在を証明）していく問題を逆分岐図問題と名付け，それを精度保証付き数値計算に基づく計算機援用証明によって解く試みについて議論する．
- 特異関数を用いた1次元エノン方程式の解の精度保証付き数値計算 / ○浅井 大晴 (早稲田大学), 田中 一成 (早稲田大学), 大石 進一 (早稲田大学) [概要]
Henon方程式の解は一般に領域内部に1つの特異点を持つため、その特異性を踏襲する近似解の構成が精度保証付き数値計算の計算コストを抑制することにつながる。特にその解曲線の描画のためには多くのパラメータに関する精度保証を行う必要があり、少ない基底関数で効率的に計算を行うことが重要となる。本講演では、ルジャンドル多項式とある特異関数を用いて近似解を構成し、ポテンシャル指数を変化させたときの多重解の精度保証結果について報告する。
- 遅延van der Pol-Duffing方程式の精度保証 / ○高松 尚輝 (早稲田大学), 齊藤 優輝 (早稲田大学), 大石 進一 (早稲田大学), 関根 晃太 (東洋大学) [概要]
本発表ではvan der Pol-Duffing方程式に遅延項と外力項を付けた方程式の解の精度保証付き数値計算法を示す．特に，本発表では分数調波解に着目し，分数調波解の存在を計算機で証明する手法を紹介する．
- 遅延van der Pol-Duffing方程式の分岐と精度保証 / ○齊藤 優輝 (早稲田大学), 高松 尚輝 (早稲田大学), 大石 進一 (早稲田大学), 関根 晃太 (東洋大学) [概要]
本発表ではvan der Pol-Duffing方程式に遅延項と外力項を付けた方程式の解の精度保証付き数値計算法の応用例を紹介する．特に，方程式の遅延時間の長さによる分岐現象の数値実験結果と分数調波解の精度保証の結果から現象を考察する．
▷ 応用カオス(3) ［3月4日：13:30-14:50：C］（座長：大久保 健一（大阪大学））
- 保存系のカオスに対する拡張型カオス尺度の計算方法の検討 / ○井上 啓 (山陽小野田市立山口東京理科大学), 真尾 朋行 (東芝情報システム株式会社・京都大学大学院), 奥富 秀俊 (東芝情報システム株式会社), 梅野 健 (京都大学大学院) [概要]
カオス尺度は、情報理論の観点からカオスを定量化する指標である。拡張型カオス尺度は、カオスにより遷移した分割要素の領域サイズを考慮するという視点をカオス尺度に追加したものであり、カオスの典型的な条件の下でリアプノフ指数の総和と一致する。しかし、軸の拡大率が大き過ぎると上記の領域サイズの見積もりが困難になる。そこで、片方の軸が拡大していく2次元の保存系に対して拡張型カオス尺度の計算方法を検討する。
- 修正カオス尺度の計算における分割の影響による離散化リアプノフ指数との誤差について / ○真尾 朋行 (京都大学大学院情報学研究科/東芝情報システム株式会社), 奥富 秀俊 (東芝情報システム株式会社), 梅野 健 (京都大学大学院情報学研究科) [概要]
カオス尺度は，カオスを定量化する指標として提案されており，得られた時系列データのみから計算可能であることを特徴としている．著者らは，カオス尺度とリアプノフ指数との差を評価・減算することによりリアプノフ指数の近似値を算出する修正カオス尺度を提案した．本発表では，修正カオス尺度の計算における分割による影響と，離散化リアプノフ指数との間に生じる誤差について調査・報告する．
- 共振周波数を用いた無線電力カラーリングとコイル配置最適化 / ○本山 雅孝 (京都大学), 梅野 健 (京都大学) [概要]
ワイヤレス給電に関して共振周波数の設定を変えることでWPC（無線電力カラーリング）の検証実験を行った。また、複数の送電コイルに対しての最適配置を実験的に確認した。
- レーザーカオスにおけるモードの同時性 / ○桑島 史欣 (福井工大), Jarrahi Mona (UCLA), CAKMAKYAPAN SEMIH (UCLA), 森川 治 (海保⼤), ⽩尾 拓也 (福井工大), 岩尾 憲幸 (福井工大), 栗原 ⼀嘉 (福井⼤教育), 和田 健司 (大阪府立大), 北原 英明 (福井⼤遠⾚セ), 中嶋 誠 (阪⼤レーザー研), ⾕ 正彦 (福井⼤遠⾚セ) [概要]
これまでの研究において、レーザーカオス光をテラヘルツ発生・検出用光伝導アンテナの励起光源として用いることで、効果的にテラヘルツ波の発生・検出が行えることを実証してきた。今回、この原因解明のため、逓倍器による他のTHｚ波源と、レーザーカオス光の光ビートをプラズモンアンテナ中で混合し、1GHz 程度のＲＦ領域にダウンコンバートし光ビートの安定性を観測したので、報告する。
▷ 連続体力学の数理(3) ［3月4日：13:30-14:50：D］（座長：井元 佑介（京都大学））
- 磁気双極子と微小円環電流の等価性を用いたHele-Shawセル内の磁性流体の運動に対するモデリング / ○下地 優作 (明治大学大学院理工学研究科数学専攻) [概要]
「磁性流体」と呼ばれる，磁場に感応しパターンを形成する流体が存在する．流体の運動を記述するNavier-Stokes方程式に磁気力を表現する外力項を加え，磁性流体の運動を再現するモデル方程式を構築し，その解の挙動について考察する．本講演では，特に「Hele-Shawセル」内での磁性流体の運動に焦点を当てる．Hele-Shawセル内の磁性流体は，3次元空間でのそれとは異なった興味深いパターンを形成する．今回は磁気双極子と微小円環電流の等価性を考慮に入れた外力項を定義し，新しいモデルを提案，そしてそれらのパターン形成の再現を試みる．
- 折れ曲がった紙に沿って拡がる燃焼前線の形状について / ○木村 桃実 (明治大学理工学研究科数学専攻), 桑名 一徳 (山形大学), 矢崎 成俊 (明治大学) [概要]
床面付近に平らに置かれた紙の燻焼現象において，
Kuramoto-Sivashinsky方程式を適用した燃焼前線の挙動の研究が近年活発になされている．
本講演では，非一様なルイス数を導入することにより，
折れ曲がった紙に沿って拡がる燻焼を想定し，燃焼前線の形状について考察する．
- ［特別講演：40分］ 接触角条件付き面積保存型曲率流に対する進行波解の安定性について / ○可香谷 隆 (九州大学マス・フォア・インダストリ研究所) [概要]
本講演では，界面エネルギーの勾配流に対応する，面積保存型曲率流と呼ばれる曲線の運動方程式を扱う．ジョルダン閉曲線に対する上記の流れは，円に漸近する性質を持つが，接触角条件を課すことによって，進行波解が安定性を持つことを紹介する．特に，本講演では，凸な解に限定すると，進行波解が大域的な安定性を持つことに焦点を当てる．この構造の違いは，エネルギー構造の変化に伴うものであり，関連しうる界面ダイナミクスについても触れる．
▷ 離散システム(3) ［3月4日：13:30-14:50：E］（座長：小林 佑輔（京都大学））
- 2次元タイトスパンの構成的判定アルゴリズムについて / ○東田 瑞己 (東京大学), 平井 広志 (東京大学) [概要]
タイトスパンは（有限）距離空間に対して定義される非凸な多面体的構造であり，生物学における系統樹構築や組合せ最適化における多品種フロー問題に応用がある．タイトスパンに関する基本的な問題として次元判定及び構成が挙げられ，1 次元の場合については効率的な方法が知られている一方で，2 次元の場合に特化した方法は現在見つかっていない．本発表では，タイトスパンの局所的な組合せ構造が 2 次元性を特徴付けることを示した上で，この特徴付けを利用した構成的な 2 次元性判定アルゴリズムについて紹介する．
- 4頂点完全グラフの根付き細分問題 / ○林 興養 (東京大学大学院情報理工学系研究科) [概要]
本発表では, 7連結なグラフにおいて, 任意に指定された4頂点を分岐点とする4頂点完全グラフの細分が存在することを示す. この結果は連結度に関して最良であり, 最近のMcCarty-Wang-Yuの結果の拡張となっている. また, 三角形を含まない6連結なグラフにおいても同様な主張が成り立つことを示し, それがMaderの予想の特殊な場合を肯定的に解決することを見る.
- ランダム部分グラフモデルにおける巨大剛体成分の解析 / ○荒川 侑馬 (東京大学), 谷川 眞一 (東京大学) [概要]
ランダムグラフ理論における代表的な話題として、巨大連結成分の解析があげられる。この巨大連結成分の類似物として1980年代に巨大剛体成分の概念が導入され、結晶の相転移のモデル化などに利用されてきた。Erdos-Renyiモデルにおいては、2010年にKasiviswanathanらによって巨大剛体成分出現の臨界確率が証明された。本発表では、より一般的なランダム部分グラフモデルを考え、Theran (2008)によるErdos-Renyiモデルに対する議論の拡張を行う。
- 周期グラフのd-実現可能性の特徴づけ / ○大場 亮俊 (東京大学), 谷川 眞一 (東京大学) [概要]
グラフGがd-実現可能であるとは任意の次元のユークリッド空間に描かれたGが辺長を変えずにd次元空間に折り畳めることをいう。d=1,2,3についてはd-実現可能なグラフの禁止マイナーによる特徴づけがBelk-Connellyによって与えられている。本発表では、d-実現可能性の概念を周期グラフへ拡張し、d=1,2についての禁止マイナー特徴づけを紹介する。
▷ 行列・固有値問題の解法とその応用(4) ［3月4日：15:00-16:20：A］（座長：佐藤 寛之（京都大学））
- 部分空間を制限する全最小二乗法の効率的な計算手法とその収束解析 / ○相島 健助 (法政大学情報科学部) [概要]
全最小二乗法は，統計における最尤推定を代表として多くの問題に応用される行列計算である．近年の問題の大規模化に伴い，全最小二乗法の応用例は多岐にわたり，入力（観測）行列および解行列に低ランク性を仮定する問題設定が増えてきている．本発表では，低ランク性および像空間に関する制約の下での全最小二乗問題を対象に，入力行列がランダムノイズを含む場合の統計解析を行うことで，効率的な計算手法を与え，その強収束を示す．
- ヒルベルト行列と関連するある行列の固有値について / ○山本 有作 (電気通信大学) [概要]
Hをs×sのヒルベルト行列とし，H’をHの各要素の分母を1ずつ増やした行列，D=diag(1, 2, …, s)として，行列K=(H’)^{-1}HDを考える。本講演では，sが2以上のとき，行列Kが必ず複素固有値を持つことを示す。Kはエネルギー保存型の常微分方程式解法であるAVF collocation法のアルゴリズム中に現れる行列であり，この結果は同解法が並列化不可能であることの1つの証明を与える。
▷ 計算の品質 (2) ［3月4日：15:00-16:20：B］（座長：関根 晃太（東洋大学））
- Kolmogorov問題に対する計算機援用証明における最大値ノルム評価とその 応用 / 小林 健太 (一橋大学), ○渡部 善隆 (九州大学) [概要]
Kolmogorov問題とは2次元Navier-Stokes方程式に特別な外力項を課した非線形偏微分方程式です。本講演ではKolmogorov問題に対する精度保証付き数値計算の過程で評価が必要となる最大値ノルムの高精度な計算方法とその応用を紹介します。
- 3次元領域におけるNavier-Stokes方程式の解の検証ライブラリの開発 / ○劉 雪峰 (新潟大学) [概要]
本研究では、Navier-Stokes方程式の解の検証に使用されるRaviart-Thomas有限要素法とScott-Vogelius有限要素法の厳密計算ライブライの開発を行っている。発表では、ライブライ開発の現状を報告し、3次元領域の計算が抱えている膨大な計算量、有限要素空間の次数が高いなど問題点の対応法を説明する。
- 不連続拡散係数を持つ３次元ポアソン方程式の解に対する事前誤差評価 / ○田中 一成 (早稲田大学), 中尾 充宏 (早稲田大学) [概要]
立方体内で定義された不連続拡散係数を持つポアソン方程式の有限要素解に対する事前誤差評価式を報告する。
拡散係数は領域内で区分的に定数であるものとし、解は各部分領域内でH2正則性を持つと仮定する。
この前提のもと、有限要素解のL2、H1、L∞ノルムの意味での構成的誤差評価を行う。
- 微分方程式のサドル型爆発解: 精度保証付き数値計算と爆発時刻の初期値連続依存性の考察 / ○松江 要 (九州大学マス・フォア・インダストリ研究所 / カーボンニュートラル・エネルギー国際研究所, 科学技術振興機構 研究開発戦略センター), Lessard Jean-Philippe (McGill University), 高安 亮紀 (筑波大学システム情報系) [概要]
微分方程式の爆発解、特に初期条件の摂動に対して不安定なものを考察します。コンパクト化、時間スケール特異点解消により、発散する解を適切に変換されたベクトル場の無限遠に対応する集合「地平線」上の不変集合の安定多様体上の軌道に対応させます。さらに不変多様体のparameterizationにより、不変集合、特に平衡点の安定性に関わらず、安定多様体の形状を局所的に解析関数として表現でき、精度保証付き数値計算も可能となります。特にparameterizationを用いた場合は爆発時刻の厳密な値の公式を得られ、シャープな評価が可能となります。これにより「爆発時刻の初期値連続依存性」を議論できるようになり、不安定な爆発解の特異性を爆発時刻の観点から議論できます。本講演ではその一例を紹介します。
▷ 数理医学 ［3月4日：15:00-16:20：D］（座長：鈴木 貴（大阪大学））
- オミクスデータを活用した肺線維症バイオマーカー探索に関する研究 / ○野島 陽水 (大阪大学 数理・データ科学教育研究センター) [概要]
特発性肺線維症（Idiopathic pulmonary fibrosis; IPF）は、特発性間質性肺炎の一種である難病である。早期発見が重要であるIPF治療であるが、その診断は専門医でも困難であり、IPFに特異的なバイオマーカーが望まれている。本研究では、これまで注目されてこなかった水溶性代謝物に着目し、メタボローム解析から新規IPFバイオマーカー候補を同定した。また公共遺伝子発現データから、その変動メカニズムの作用機序をモデル化したので、これを報告する。
- 医療保険数理の改善について / ○村山 令二 (健康保険組合連合会) [概要]
医療保険制度における計量的な側面は医療保険数理または単に保険数理と呼ばれている。
近年、医療保険数理において、差分方程式・微分方程式を用いた新しいレセプト分析手法と、連立常微分方程式の逆問題を用いて、複数要因からなる変数の長時間の変化について各要因の寄与を公平に算定する新しい手法が開発され、これらの手法を用いた分析結果が定期的に公表されている。本講演では、これらの新しい手法とその意義について報告する。
- 医療費の公平寄与率の定義と一意性について / ○鈴木 貴 (大阪大学 数理・データ科学教育研究センター) [概要]
医療費の年度ごとの全体コスト変動から、各成分の寄与（ミクロ寄与率）を決定する問題について厚労省が用いている公式を分析する。マニュアルに従って公平寄与率を定義すると、いくつかの集計方法において公式が唯一のものであることがわかる。
▷ 数理政治学 ［3月4日：15:00-16:20：E］（座長：大山 達雄（政策研究大学院大学））
- 動的モデルによる救急隊配置の最適化手法―山形県酒田地区におけるケーススタディ / ○川崎 雄二郎 (京都先端科学大学), 萩原 茂樹 (公立千歳科学技術大学), 三木 潤一 (東北公益文科大学) [概要]
本研究では、日本の救急サービスの実態に基づいて救急の動的モデルを構築し、実データに基づいて、救急隊の最適配置を求める新たな手法を開発する。提案するモデルは、各救急事案に出動する救急隊の逐次決定過程を実態に沿って精密に表現するものである。ケーススタディとして山形県酒田地区で発生した救急事案データに適用した結果、本手法の有効性が確認された。
- Koopman 作用素を利用した発展型ネットワーク予測の試み / 徐 百歌 (神戸大学大学院システム情報学研究科), ○谷口 隆晴 (神戸大学大学院システム情報学研究科) [概要]
Koopman作用素を利用したシステム解析は，有限次元の非線形なダイナミクスを無限次元の線形作用素の性質を通して理解しようとする手法である．特に，この作用素を推定することが出来れば，ダイナミクスの予測なども可能となる．本研究では，この手法を用いて，時間発展型のネットワークの予測やその性質の解析を行う．
- レバレッジを伴う繰り返し投資は破産を避けられない運命にある / ○新居 桃佳 (静岡大学総合科学技術研究科), 守田 智 (静岡大学総合科学技術研究科) [概要]
本研究は近年における金融業務の急速なエレクトロニクス化とそれに伴う市場のグローバル化によりみられるようになったレバレッジを伴う繰り返し短期投資戦略と破産確率との関係性について調べ、この投資戦略において投資取引一回あたりの破産確率を無視することの危険性について論ずる。
- Twitterネットワークを模した有向ネットワークを生成するシミュレーションモデル / ○前原 風太 (静岡大学大学院総合科学技術研究科), 守田 智 (静岡大学大学院総合科学技術研究科) [概要]
現在Twitterはコミュニケーションツールとして広く使われている。それは独自のネットワークを築いていて、wwwや友人関係のネットワークと性質が異なると思われる。本研究ではその点を考慮しつつバラバシ・アラバートを有向方向に拡張し、優先的選択以外の要素を加えつつTwitterネットワークを再現するモデルを考案する。
▷ 特別講演 ［3月4日：16:30-17:50：A］（座長：時弘 哲治（東京大学））
- 研究部会連合発表会のひとまわりを祝って / ○中村 佳正 (京都大学) [概要]
「研究部会連合発表会」は春の応用数理学会としてすっかり定着してきました。できたての博士学位論文や修士論文など若手研究者の登竜門としても機能していると思います。応用可積分系研究部会担当から始まってまた応用可積分系研究部会担当に一巡して戻ってきた「研究部会連合発表会」の成功を祝って、立ち上げの経緯などを含めてご挨拶させていただきます。
- 可積分系と幾何学的形状生成ー「よい」方程式は「よい」形状を生成するか？ー / ○梶原 健司 (九州大学マス・フォア・インダストリ研究所) [概要]
19世紀の古典微分幾何学は古典力学と同様に可積分系の源で，例えばガウス曲率が負の一定値を取る曲面（擬球曲面）はsine-Gordon方程式で記述される．また，オイラーの弾性曲線は，曲率が平面曲線の弧長を保つ変形を記述するmKdV方程式の進行波解で特徴付けられる．最近，工業意匠設計分野で車のデザイナーが美しいと見なす平面曲線の族「対数型美的曲線」が弾性曲線の相似幾何類似と同定された．曲線族はBurgers方程式の進行波解で特徴付けられる．現在，それを足がかりに空間曲線や曲面への一般化が研究されており，曲面は擬球曲面の相似幾何類似と見なすことができる．可積分系は「よい」形状を生成するだろうか？
- 可積分系研究の可能性 / ○西成 活裕 (東京大学) [概要]
可積分系の研究はこれまで日本人の貢献が著しく、日本が世界に誇れる分野の一つといえる。そして理論研究に加え、様々な応用研究も進められてきた。講演ではこれまで応用研究を行ってきた経験から、今後のチャレンジすべき分野についての展望について述べたい。
- ファジーCAの解析 / ○薩摩 順吉 (武蔵野大学) [概要]
０と１の値をとる基本的セルオートマトンの変数の値を実数に拡張した非線形差分方程式をファジーCAという。本講演ではいくつかのファジーCAの解について解析的な考察を加える。また、本研究の意義についてコメントするとともに、超離散化との関連についても触れる。
▷ CAEモデリングとデータ活用 ［3月5日：09:40-11:00：A］（座長：山田 知典（東京大学））
- 骨格線とFunctional Map法を用いた表面メッシュの対応点構築 / ○山本 晶偉 (中央大学理工学部), 森口 昌樹 (中央大学理工学部) [概要]
二つの表面メッシュ間の対応点関係を構築することはテクスチャや変形の転写等に応用できる重要な形状処理技術であり、Functional Map法は効率的に対応点関係の構築が行える手法である。しかし入力となるメッシュは等長変換の関係にあることが望ましく、非等長変換下では構築される対応点の精度が低下する。本研究では骨格線の情報を利用することで、等長に近い変換、非等長変換下での精度改善を行った。
- 機械学習を活用した設計チェックルール作成技術の開発 / ○片岡 一朗 (日立製作所) [概要]
- CAEサロゲートモデル構築のためのデータ拡張と正則化手法の検討 / ○和田 義孝 (近畿大学) [概要]
物理現象のサロゲートモデルの構築は微分方程式で表現されているとはいえ特異性や急激な変化を伴うことがありどこまで精度を求めるのか設定することすら困難である。その問題に適したパラメータを予測するほうが一般には良い結果が得られる。一方で、機械学習を用いる場合どの程度の学習データを準備できるか重要な問題である。本報告ではデータ拡張を前提として少ないデータで学習した場合、正則化手法が予測に与える影響を評価する。
- デジタル打音検査におけるシミュレーションと機械学習 / ○山田 知典 (東京大学) [概要]
コンクリート構造物に多い変状としてかぶりコンクリートの剥落があり，主たる要因として施工時の欠陥が指摘されている．打音検査は，欠陥の有無を短時間で評価できるが，欠陥の種類を識別し，その深さや大きさ等を定量評価するまでに至っていない．本発表ではこれを実現するために，デジタル打音検査とシミュレーション，機械学習を用いた取り組みについて述べる。
▷ 計算の品質 (3) ［3月5日：09:40-11:00：B］（座長：山中 脩也（明星大学））
- エラーフリー変換を用いた悪条件行列の生成法 / ○尾崎 克久 (芝浦工業大学), 荻田 武史 (東京女子大学) [概要]
本発表では，すべての成分が浮動小数点数である悪条件行列の生成法について述べる．クロネッカー積の性質と浮動小数点数のエラーフリー変換をうまくあわせ，条件数をある程度正確に設定でき，固有値・固有ベクトルに関する情報も低コストで出力できる手法を開発した．
- DE-Sinc関数近似の刻み幅と打ち切り数の決定式の改善と理論誤差評価 / ○小川 翔大 (広島市立大学), 岡山 友昭 (広島市立大学) [概要]
DE-Sinc関数近似は非常に高性能な関数近似公式として知られている．また，その近似結果を精度保証するためには近似公式の厳密な誤差上界を評価する必要があるが，実際にそれが可能な理論誤差評価も与えられている．さらに後藤は，刻み幅の決定式を工夫することで改善した誤差評価を与えているが，本研究では後藤の方法に対し刻み幅や打ち切り数の決定式をさらに工夫し，より厳しい誤差評価を与える．
- 疎行列に対する逆行列のノルムデータとその活用法 / ○尾崎 克久 (芝浦工業大学), 荻田 武史 (東京女子大学) [概要]
SuiteSparse Matrix Collectionは多くのテスト行列を収集してあるよく知られたサイトである．このサイトにある行列の逆行列に関し，最大値ノルムの上限を計算したことをまず報告する．またそのデータの活用法として，疎行列を係数とする連立一次方程式の解の精度保証法について紹介する．
▷ 応用可積分系(1) ［3月5日：09:40-11:00：C］（座長：延東 和茂（早稲田大学））
- ファジーセルオートマトンの漸近解について / ○山本 航 (早稲田大学基幹理工学部), 高橋 大輔 (早稲田大学基幹理工学部) [概要]
ファジーセルオートマトン(fCA)は，ファジー論理によってCAを連続化して得られる時間発展の系である．本講演では，三近傍一階のECAの時間発展則を多項式によりファジー化した系の時間発展について，時間無限大での漸近解に焦点を当てて議論する．
- 完全1次保存する非自明な3値3近傍ファジーCAの収束性 / ○西田 優樹 (同志社大学大学院理工学研究科), 山﨑 功貴 (同志社大学大学院理工学研究科), 渡邉 扇之介 (福知山公立大学情報学部), 福田 亜希子 (芝浦工業大学システム理工学部), 渡邊 芳英 (同志社大学理工学部) [概要]
3値3近傍セルオートマトン(CA)は，セルのとる値を3次元ベクトルで表現することで局所遷移関数の多項式表現を通してファジー化できる．また3値3近傍ファジーCAにおいて，ベクトルの成分が完全1次保存するルールは全部で15通り存在する．特に，その中で非自明な挙動を示すものは2つのクラスに分けることができる．本講演ではこれらのファジーCAの漸近挙動を調べ，その収束性について数学的な証明を与える．
- ファジーセルオートマトンルール184へ慣性の効果を取り入れた拡張 / ○東 康平 (東京大学大学院数理科学研究科) [概要]
Slow-to-startモデル（Takayasu-Takayasu 1993）は，相転移現象を示す交通流のセルオートマトンモデルとして注目されてきた．
本講演では，このモデルをファジー化したものが，ファジーセルオートマトンルール184に慣性の効果を取り入れた拡張モデルになることを示し，ファジー化に伴う自由度による分類と，それらの定常解，安定性や基本図の性質について紹介したい．
- 相関付きランダムウォークから導かれる超離散バーガースセルオートマトン / ○渡邉 扇之介 (福知山公立大学), 福田 亜希子 (芝浦工業大学), 瀬川 悦生 (横浜国立大学) [概要]
ランダムウォークの拡張として知られる相関付きランダムウォークの発展方程式を超離散化し，超離散コール・ホップ変換を行うことで超離散バーガース方程式のある拡張が得られる．本講演では，この拡張された超離散バーガース方程式がある条件の下でセルオートマトンとなることを示し，交通流モデルへの応用について議論する．
▷ 幾何学的形状生成 (1) ［3月5日：09:40-11:00：D］（座長：大崎 純（京都大学））
- 曲線折りのシミュレーションによって得られる幾何形状の評価手法 / ○佐々木 好祐 (筑波大学), 三谷 純 (筑波大学) [概要]
Ruling配置を考慮した展開図の三角形分割によって生成された三角形メッシュを用いることで、曲線折りのシミュレーションができる。本発表では、そのような曲線折りのシミュレーションの結果得られるモデルの可展性や曲面の滑らかさを計測する評価指標をいくつか紹介する。また、実際にそれらの手法を用いて評価を行った結果を報告する。
- 曲線折りの形状モデリングにおけるrulingの交差の回避手法とその改善 / ○大橋 芳 (筑波大学), 三谷 純 (筑波大学) [概要]
曲線折りの形状をモデリングする際、ruling同士が交差してしまう問題がある。従来のシステムでは、このような交差を回避するためにユーザが複数のパラメータを手作業で修正する必要があった。そこで、本研究ではruling同士の交差を自動で回避する手法を提案する。提案手法では、交差の程度を表す評価関数と形状の違いを表す評価関数を定義し、それらの重みづけ線形和を最適化問題として解く。
- 正多角形を縮小するように折りたためる剛体かつ厚みのあるリンク機構の生成手法 / ○山本 陽平 (筑波大学 システム情報工学研究科), 三谷 純 (筑波大学 情報システム系) [概要]
折り紙の技術は，折りたたみと展開による伸縮機構を持つ構造物に活用できる．ただし、活用される折りのパターンは，剛体かつ厚みのある素材を折りたためる必要がある．本発表では，この条件を満たす相似な形に折りたためる正多角形を，既存の折りパターンの一部にスリットを加えることで生成する．生成に必要なパラメータを明らかにし，最急勾配法を用いて，より小さく折りたためる折りパターンを生成した．
- 法線マップ画像の色調変更による可展面の変形操作 / ○舟久保 拓哉 (筑波大学), 三谷 純 (筑波大学) [概要]
可展面とは曲面の一種であり、歪みなく平面に展開できるような形状を指す。なおここでは折り目を含まないものを扱う
また、法線マップとは法線ベクトルの(x,y,z)情報を、画素の(R,G,B)の値に対応させたものである。本手法では法線マップを用いて可展面を編集することを目的とする。入力可展面から取得した法線マップを画像処理し、画像処理された法線マップを元に出力される可展面の法線方向を決定することで可展面を編集する。
▷ 数理設計(1) ［3月5日：09:40-11:00：E］（座長：代田 健二（愛知県立大学））
- 密度法に基づくトポロジー最適化解析に対する重み付き感度の適用 / ○岸田 真幸 (長岡技術科学大学大学院 技術科学イノベーション専攻), 倉橋 貴彦 (長岡技術科学大学大学院 機械創造工学専攻), Baiges Joan (Barcelona School of Civil Engineering, Polytechnic University of Catalonia) [概要]
本研究では，非定常振動問題におけるひずみエネルギー最小化を目的とした密度型トポロジー最適化を実施した．その最適化の中で用いる感度に対して可変的な重みづけを行った．本講演では，重みづけ感度によるチェッカーボードの抑制の結果について報告する．
- 平均コンプライアンス最小化問題への加速射影勾配法の適用 / ○西岡 暁 (東京大学), 寒野 善博 (東京大学) [概要]
本研究では、現在機械学習分野を中心に盛んに研究されている加速射影勾配法（加速近接勾配法）を、代表的なトポロジー最適化問題である平均コンプライアンス最小化問題に適用する。本手法は、停留点への収束性が保証されている。また、有限要素数が多い場合に、代表的な解法である最適性基準法と比べて停留点近傍での収束が速いことを示す。
- 椎体の形状変形に基づく骨量増減同定 / ○三本 康貴 (名古屋大学), 畔上 秀幸 (名古屋大学) [概要]
本研究は，特発性側彎症の成因を探るために，患者脊柱の医用画像データから骨量の増減量を同定する問題を定式化して，その解法を示すことを目的としている．本発表では，基本的な形状変動から骨量の増減量に相当する非弾性ひずみが同定され，逆に，それが発生したときに最初の形状変動が再現できることを確認する．
- 流体構造連成を考慮した幾何学的非線形構造物の形状設計 / ○片峯 英次 (岐阜工業高等専門学校), 河合 竜雅 (長岡技術科学大学), 高橋 みのり (岐阜工業高等専門学校) [概要]
定常流体構造連成を考慮した幾何学的非線形構造領域において，部分境界での変位をコントロールする形状設計問題の数値解析法を提案する．形状設計問題を定式化し，随伴変数法を利用して，領域変動に対する形状修正の感度（形状勾配関数）を理論的に導出する．導出された形状勾配関数に基づいて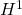
勾配法を適用し，Freefem++を利用して数値解析した簡単な二次元の解析例を紹介する．
▷ 数理ファイナンス(1) (10:00~) ［3月5日：09:40-11:00：F］（座長：関根 順（大阪大学））
- 経済指標の予測と、それを応用した投資戦略について / ○金子 拓也 (国際基督教大学), 美嶋 勇太朗 (株式会社KDDI総合研究所、KDDI株式会社), 木村 塁 (KDDI株式会社), 和田 真弥 (株式会社KDDI総合研究所), 大角 良太 (トヨタ自動車株式会社), 斎藤 紀明 (トヨタ自動車株式会社) [概要]
本研究では、まず保有するデータを活用していくつかの経済指標を予測する方法を考える。つぎにその予測結果に基づいて投資戦略を組み立てたときの有効性について実際のデータで検証する内容となっている。
- わが国の卸電力取引における数量制約付き通告変更権の価値評価 / ○遠藤 操 (電力中央研究所) [概要]
本研究では，卸電力取引における通告変更権(スイング・オプション)について，一定期間内に変更できる量に制約がある場合の価値評価を行う．常時需給の一致が必要とされる電力市場において，卸取引の通告変更権は需給調整のための重要なオプションであり，火力電源に設定されることが多い．発電用燃料(特にLNG)の調達契約における数量制約が権利行使量の制約となっており，本研究では実際の取引条件を想定した価値評価計算を行う．
- 日本の株式市場に対するG-VaRの適用 / 青木 智春 (法政大学理工学部), ○安田 和弘 (法政大学理工学部) [概要]
Peng et al. (2020)でSublinear expectationの理論を用いたVaR（G-VaR）の計測方法が提案されており，ナスダック総合指数とS&P500のデータに対してロバストな結果を得ている．本講演では，日本のいくつかの指数や個別株にG-VaRを適用した結果を紹介し，その適用可能性や問題点などについて述べていく．
▷ 科学技術計算と数値解析(1) ［3月5日：11:10-12:30：A］（座長：岡山 友昭（広島市立大学））
- 指数的減衰関数の半無限積分に対し複合台形則と組み合わせる二つの変数変換の優劣の理論解析 / ○廣畑 克哉 (広島市立大学), 岡山 友昭 (広島市立大学) [概要]
指数的減衰関数の半無限積分に対し，変数変換によって全無限積分に変形した後に複合台形則を適用する計算法があり，LundとMuhammad-Moriによってそれぞれ別の変数変換が提案されている．先行研究では二つの変数変換の比較をして，Muhammad-Moriの方がよい場合があるとしているが，常に良いとは示されていなかった．それに対し本研究では，Muhammad-Moriの方が常に良いことを示した．
- 非凸領域における境界値問題に対する局所誤差評価 / ○中野 泰河 (新潟大学大学院自然科学研究科), 劉 雪峰 (新潟大学大学院自然科学研究科) [概要]
本研究では、これまでに検討した有限要素解の局所誤差評価法を拡張し、領域の非凸性に伴う境界値問題の解の特異性にも対応できる新たな局所誤差評価法を提案する。
本講演では，非凸領域における境界値問題の局所誤差解析の数値例によって、提案手法の有効性を報告する。
- 固有直交分解法とGalerkin射影に基づく縮約モデルの配管系流れ解析への適⽤ / ○矢敷 達朗 ((株)日立製作所), 奥田 洋司 (東京大学新領域創成科学研究科) [概要]
配管系を対象とした3次元流体解析の計算時間短縮を目的として、縮約モデルの配管系流れ解析への適用を目指している。本発表では、配管内旋回流れ解析結果に固有直交分解法とGarlerkin射影を適用して縮約モデルを構築し、縮約モデルを用いた流れ解析の計算精度、計算時間短縮の効果を検討した結果を紹介する。
- 構造力学における薄板理論の直交選点有限要素法(OCFEM)による定式化と数値計算 / ○大久保 孝樹 (函館高専) [概要]
薄板理論のOCFEMによる定式化では、たわみに関する4階の偏微分方程式を扱わなければならないが、4変数(たわみv、モーメント：Mx, My, Mxy)の連立2階偏微分方程式に変換すると、容易にOCFEMで定式化することが可能となる。このようなたわみと3つのモーメントによって、境界条件の設定が容易になる部分が出てくる。等分布荷重においてOCFEMとフーリエ級数解を比較し有効数字７桁程度の一致が見られた。
▷ 折紙工学(1) ［3月5日：11:10-12:30：B］（座長：三谷 純（筑波大学））
- 「折り」を生かした立体芸術「扇」の歪みの数理的解明と画像処理を利用した扇復元の試み / ○山崎 桂子 (明治大学), 阿部 富士子 (明治大学), ディアゴ ルイス (明治大学), 萩原 一郎 (明治大学) [概要]
日本発の扇は扇型の平面画を蛇腹に折って骨に差し，扇の上下で収縮率の異なる立体構造として仕立てるため，その扇面は歪む．その歪みは扇の骨の長さ等の各種のパラメータに依存する．扇をデジタルに取り込めば非接触で様々な角度から調査することが可能になる．本研究では開発した数理モデルを用いて扇を折上げ，また逆に扇を極めて正確な平面画に変換することによって，写真画像からの扇の復元及び扇のレプリカ作成を試みる．
- 伸縮・曲げ・回旋する剛体折紙機構 / ○上條 陽斗 (東京大学), 舘 知宏 (東京大学) [概要]
剛体折紙で構成された合同なモジュールを線状に連結させることで3自由度の機構を構築する。鏡映を用いて連結することでモジュールの個数を増やしていっても3自由度を保つ。この機構は全体として円弧を描き、全体が連動しながら伸縮、曲げ、方向を連続的に変化させる事ができる。この機構の運動学を解析し、得られる伸縮・曲げ・方向の範囲について明らかにした。また本機構が、折りを使って平面から簡易に製造可能であることも示す。
- 平行四辺形二面体の最小跡と最遠点写像 / ○山岸 義和 (龍谷大学) [概要]
平行四辺形二面体の source unfolding は、多くの場合、十角形となる。多面体上に与えられた点からの最遠点は、最小跡の頂点の一つとして得られる。最遠点写像の極限によって多面体の直径が得られるかという問題を考える。平行四辺形二面体の場合、60度より小さい内角を持つときは最遠点写像の極限によって直径が得られる。
- 厚みを持つ折り紙の運動経路に関する基礎的研究 / ○張 天昊 (東京大学), 川口 健一 (東京大学) [概要]
折り紙は建築を含む種々の工学の分野で活用が期待されているが、実用化を目指すには材料の厚みを考慮することが重要である。本研究では、一般逆行列を用いた手法に基づき、形態不安定な骨組構造の剛体運動を計算することで厚みを持つ折り紙の運動経路を追跡する方法を提案する。
▷ 応用可積分系(2) ［3月5日：11:10-12:30：C］（座長：渡邉 扇之介（福知山公立大学））
- 確率バーガースセルオートマトンの定常分布の証明と分解仮設 / ○延東 和茂 (早稲田大学), 田中 悠太 [概要]
著者は以前確率バーガースセルオートマトン(SBCA)の定常分布について、各状態の確率比が空間内の特定のパターン数に応じたべき乗によって導出されると予想した。本講演では予想した定常分布の証明を紹介する。さらに、分解仮設と呼ばれる系の定常状態における物理量の導出に用いられる仮設と、証明された定常分布との関係について論じる。また、SBCAの時間高階拡張系の定常分布の予想についても紹介する。
- max-plus版およびセルオートマトン版Leniaモデルについて / ○高橋 大輔 (早稲田大学理工学術院) [概要]
Leniaは人工生命モデルのひとつであり、近傍値を表す核関数と、近傍値による成長を表す成長関数から成り立っている。これら関数をmax-plus関数で置き換えることにより、max-plus版のモデルを得ることができる。さらに、パラメータを特殊化することによりセルオートマトン版のモデルも得られる。講演では、これらのモデルの解の振る舞いについて、オリジナルのLeniaと比較しながら議論する。
- 空間依存Nicholson-Baileyモデルのmax-plus化について / ○太田 順也 (早稲田大学), 高橋 大輔 (早稲田大学) [概要]
Nicholson-Bailey (NB)モデルは生態系の種間の相互作用に関する数理モデルであり，空間依存性を付与した拡張版も報告されている．この空間依存NBモデルでは指数関数を含む相互作用と近傍の状態値平均が用いられており，解は興味深い時空間パターンを示す．本講演では，このモデルの仕組みをmax-plus演算に置き換えた系について述べ，解の振る舞いなどを議論する．
- 可解max-min方程式の解構造について / ○北川 宗詢 (早稲田大学大学院基幹理工学研究科数学応用数理専攻高橋研究室修士課程1年) [概要]
max, minと符号反転で定義される1+1次元時間発展方程式について，解の複雑度が時間に対して多項式オーダーになる，いわゆる可解クラスに属すると思われる方程式が報告されている．本講演では，このような方程式の解構造における共通の仕組み，および，それに基づく一般形について述べる．
▷ 幾何学的形状生成 (2) ［3月5日：11:10-12:30：D］（座長：梶原 健司（九州大学））
- Gaussian curvature flowによる区分的にガウス曲率一定な離散曲面の建築形態創生 / ○林 和希 (京都大学), 軸丸 芳揮 (九州大学), 大崎 純 (京都大学), 可香谷 隆 (九州大学), 横須賀 洋平 (鹿児島大学) [概要]
建築形態創生のためにGaussian curvature flowを用いて区分的にガウス曲率が一定の離散曲面を生成する方法を提案する。
曲面のエネルギー汎関数をまず定式化し、その停留点が平均曲率とガウス曲率の荷重和が一定のLinear Weingarten(LW)曲面であることを示す。
エネルギー汎関数の停留条件から各節点のガウス曲率を指定値に近づけるための勾配流を求め、様々な形状の曲面に適用する。
- Ricci Flowに基づいた可展離散曲面の生成法 / ○張 景耀 (京都大学), 大崎 純 (京都大学) [概要]
Ricci flowは、初期曲面を指定曲率に等角写像させる強力なツールである。特に、指数的収束性を有するため、Ricci flowは、曲面レジストレーションのために平面（曲率ゼロ）に展開するなど、幅広く応用されている。本研究では、（内部）可展の離散曲面を生成するために、Ricci flowに基づいた手法を提案する。
- 離散曲面の幾何学的不変量を用いた曲面分割手法の曲面構造への応用 / ○早川 健太郎 (京都大学), 大崎 純 (京都大学) [概要]
特定の荷重条件において，面内応力のみで釣り合う曲面と平均曲率一定曲面は等価であることが知られている。そこで，離散曲面の平均曲率にもとづき，平均曲率が一定に近い複数の曲面を接続して与えられた曲面を近似し，得られた曲面の力学性能の検証を行う。
- リー球面幾何による離散曲率線グリッドシェル構造の形状決定法 / ○横須賀 洋平 (鹿児島大学), 井ノ口 順一 (筑波大学), 大崎 純 (京都大学), 本間 俊雄 (鹿児島大学) [概要]
本稿では、リー球面幾何に基づく離散曲面を用いた離散曲率線によるグリッドシェル構造を提案する。離散曲面の主曲率方向を細分化することで、誤差がなく区分的に滑らかな離散曲率線を構成したグリッドシェル構造を構築する。離散曲率線によるグリッドシェル構造は、一軸の曲げ加工のみで湾曲した曲線部材を製作することができる優れた施工性・製作性を有することを示す。
▷ 数理設計(2) ［3月5日：11:10-12:30：E］（座長：中澤 嵩（大阪大学））
- Karhunen-Loève 展開によるモデル次数低減を用いた形状最適化解析の高速化 / ○下元 翼 (名古屋大学), 丹後 秀一 (名古屋大学), 畔上 秀幸 (名古屋大学) [概要]
本研究は，H1勾配法による形状最適化解析の中でも計算時間の大部分を占める有限要素解析について，Karuhunen-Loéve 展開による計算次元の縮退を適用することによってより高速なアルゴリズムを開発することを目的としている．本発表ではH1勾配法による形状最適化に縮退を組み込む手法を紹介するとともに，線形弾性，超弾性のふたつの解析条件について上記の手法を適用した結果を示す．
- 微圧縮性を考慮した熱対流場における形状最適化 / ○青木 崇 (長岡技術科学大学大学院 機械創造工学専攻), 倉橋 貴彦 (長岡技術科学大学大学院 機械創造工学専攻), 片峯 英次 (岐阜工業高等専門学校 機械工学科) [概要]
本研究では，熱対流場において放熱量の最大化を目的とし，微圧縮性を考慮した場合の形状最適化を実施した．微圧縮性の効果として，運動方程式の圧力項および粘性項における係数である密度を温度による関数とした．本講演では，微圧縮性を考慮した場合の放熱量の最大化の結果について示す．
- 微分作用素の固有関数の誤差評価と形状最適化への応用 / ○劉 雪峰 (新潟大学) [概要]
本研究では、微分作用素の近似固有関数に対する誤差評価を検討し、既存のDavis-Kahanの評価方法より、固有関数の正則性への要求を緩和し、弱形式で定義された固有関数の誤差評価方法を提案した。さらに、固有関数の厳密評価による微分作用素の固有値の最小化問題を考え、形状最適化の問題への応用を検討した。
- 超弾性体の終端平均コンプライアンスに対する領域積分型形状微分 / ○畔上 秀幸 (名古屋大学) [概要]
超弾性体の剛性を最大化する形状最適化問題は，体積制約の下で終端平均コンプライアンスを最小化する問題として定式化される．終端平均コンプライアンスは，有限変形に対して定義された外力仕事から強制変位による仕事を差し引いた汎関数として定義される．これまで，この形状微分は境界積分形式で導出されていた．本発表では，領域積分形式の形状微分を導出する方法を示す．
▷ 数理ファイナンス(2) ［3月5日：11:10-12:30：F］（座長：畑 宏明（一橋大学））
- The existence and uniqueness of a solution to Double Barrier Backward Doubly Stochastic Differential Equations / ○林 匡史 (三菱UFJ信託銀行) [概要]
Double barrier backward doubly stochastic differential equations (DB-BDSDEs, for short) are equations with two different directions of stochastic integrals, i.e., the equations involve both a standard “forward” stochastic integral and a “backward” stochastic integral with two mutually independent standard Brownian motions, and with two reflection barriers. This kind of equations is a joint version of backward doubly stochastic differential equations (BDSDEs, for short) and double barrier backward stochastic differential equations (DB-BSDEs, for short). The former has been introduced by Pardoux and Peng. They have proved the connection with a class of systems of quasilinear SPDEs and the existence and uniqueness result of such PDEs. The latter has been tackled by Hamadene et al. In this talk, we try to show the outline of the proof for the existence and uniqueness of a solution to DB-BDSDEs by using the “penalization method”, so-called under appropriate conditions. At the end of this talk, we introduce our next study that we are tackling now.
- BSDEs driven by multi-dimensional random walk on a lattice: convergence analysis via Wasserstein Central Limit Theorem / 関根 順 (大阪大学基礎工学研究科), 深澤 正彰 (大阪大学基礎工学研究科), 安藤 眞志 (大阪大学基礎工学研究科), ○田中 章博 (大阪大学基礎工学研究科/三井住友銀行) [概要]
デリバティブの評価において、XVAと呼ばれる評価調整を加味しプライシングすることが市場慣行になりつつあり、実務において段階的に対応が進められている。一方、XVAはBSDEの解を用いて定義されることから、数値計算が難しく、近似的な手法で計算されている。本研究では、格子上のランダムウォークを用いたBSDEの近似について紹介する。
- スパースグリッドを用いた後退確率差分方程式の数値解法の研究 / ○兼子 晃寛 (大阪大学) [概要]
後退確率差分方程式 (BS∆E) は、その連続時間版である後退確率微分方程式と比べノイズ過程の従う分布に関して自由度が高く、様々な応用可能性を持つ。ところが、実用に足るBSΔEの数値解法はあまり開発されてはいない。本研究では、一次元アルゴリズムの効率的高次元化手法であるスパースグリッド法を用いた高次元BSΔEの数値解法を開発した。また、開発手法の効率性を評価するための誤差解析を実施した。
- 資産構成制約を考慮したベンチマーク追尾型ポートフォリオ最適化 / ○家田 雅志 (東京理科大学) [概要]
本講演では、空売り禁止制約およびレバレッジ制約を考慮した連続時間ベンチマーク追尾型ポートフォリオ最適化問題を確率制御により定式化し、導出される Hamilton-Jacobi-Bellman 方程式に対する数値解析結果について報告する。
▷ 科学技術計算と数値解析(2) ［3月5日：13:30-14:50：A］（座長：山本 野人（電気通信大学））
- Runge-Kutta法によるMorse分解の近似計算の性能 / ○千葉 悠喜 (明治大学), 宮路 智行 (京都大学), 小川 知之 (明治大学) [概要]
Conley-Morseグラフの手法はset-orientedな数値計算によって力学系の相空間構造を回帰的な成分とそれらの間の勾配的な構造として記述する．常微分方程式で定義される力学系に対して適用する手法として，我々は近似計算に基づいてMorse分解を計算する方法を提案した．既存の手法と比べ，数学的な厳密性は犠牲になるものの，相空間構造を理解する上での実用性の向上が期待される．本講演では，既存の手法と我々の提案手法について，計算コスト等の比較を行う．
- 2段1次のImplicit-Explicit ルンゲークッタ法の安定性 / ○大野 博 (茨城大学) [概要]
Implicit-Explicit ルンゲークッタ法(IMEX-RK)は、常微分方程式の陰的な部分と陽的な部分を分けて数値計算する手法である。IMEX-RK法の絶対安定領域は、陰的な部分がA-安定になるとき陽的な部分を複素平面上に描いたものとする。2段1次IMEX-RK法の絶対安定領域について考える。この場合、絶対安定領域が複素平面の原点を含まないものが存在する。絶対安定領域が大きくなる条件を示す。
- 行列Mittag-Leffler関数に対する精度保証付き数値計算と非整数階微分方程式への応用 / ○宮島 信也 (岩手大学) [概要]
We propose two algorithms for numerically calculating interval matrices including two-parameter matrix Mittag-Leffler (ML) functions. We first present an algorithm for computing enclosures for scalar ML functions. Then, the two proposed algorithms are developed by exploiting the scalar algorithm and verified block diagonalization. The first algorithm relies on a numerical spectral decomposition. The cost of this algorithm is only cubic plus that of the scalar algorithm if the second parameter is not too small. The second algorithm is based on a numerical Jordan decomposition, and can also be applied to defective matrices. A numerical experiment illustrates an application to a fractional differential equation.
- 離散力学系非双曲型不動点近傍でのLyapunov関数の精度保証による構成について / ○皆本 啓吾 (電気通信大学), 新田 光輝 (電気通信大学), 山本 野人 (電気通信大学) [概要]
離散力学系の非双曲型不動点近傍でのLyapunov関数を精度保証法によって構成することを試みる。ここでは、2次元離散力学系を扱い、線形化方程式の係数行列が直交行列となる場合に限定して考える。提案する手法は、連続力学系の非双曲型平衡点近傍のLyapunov関数の構成法を参考にして導いたものである。講演では、その適用範囲について考察し、適用例を数値例として提示する。
▷ 折紙工学(2) ［3月5日：13:30-14:50：B］（座長：石田 祥子（明治大学））
- 複数の固有値制御を目指した新しい位相最適化手法の開発とその折紙構造への適用 / ○佐々木 淑恵 (明治大学 先端数理科学インスティテュート), 萩原 一郎 (明治大学 先端数理科学インスティテュート) [概要]
困難であった位相最適化が可能となって30年、これまで多くの研究がなされているが、とても設計には利用できない形状が得られたで終わっている。この方法で実際の設計まで持って行くことは特に複数の固有値制御の課題に対しては困難である。本研究は振動の原点に立ち返り新しい位相最適化の提案を行い、折り紙構造に適用しその有効性を示す。
- 遮音特性シミュレーションの理論的検討と吸音材貼付折紙コアへの応用 / ○阿部 綾 (明治大学), 屋代 春樹 (明治大学), 萩原 一郎 (明治大学) [概要]
有限要素法で遮音特性が評価できれば研究効率が上がるが理論解とは合致しなかった。剛体に近いモデルでその原因究明を示してきた。ただこれまでの手法では、吸音材が貼付されたモデルなど剛体とみなすことが困難なモデルには使用できない可能性がある。そこで本報では差分解と有限要素解の組み合わせで手法の汎用化を行い、その有効性の確認と遮音に対する新たな知見を目指す。
- Waterbomb Tessellationによる波状曲面の数理 / ○今田 凜輝 (東京大学), 舘 知宏 (東京大学) [概要]
折紙テッセレーションが形成する離散曲面は、折り目の周期性からは非自明な挙動をなすことで注目されている。特に、Waterbomb Tessellationを円筒状に丸めたWaterbomb Tubeは波状の曲面になり得ることが報告されているが、この現象が生じる理由・条件は未解明であった。本発表では特にモジュールの幾何に着目し、剛体折紙・初等幾何・力学系等の知識を駆使してこれまでに得られた、現象の背景数理に関する知見を述べる。
- フォーム充填二重構造の衝撃エネルギー吸収特性 / ○楊 陽 (明治大学), 趙 希禄 (埼玉工業大学), 孔 呈海 (トピー工業株式会社), 戸 倉直 (（株）トクラシミュレーションリサーチ), 萩原 一郎 (明治大学) [概要]
車の衝突時のエネルギー吸収や落石の運動エネルギーの吸収に最も効率の良い方策は、柱構造を軸方向に潰すことである。エネルギー吸収性能の向上が望まれ、また環境問題等の点から軽量化構造の開発も大きな研究課題となっている。高いエネルギー吸収特性を効率良くかつ重量増加 を抑えながら実現するために、フォームを充填した構造部材のエネルギー吸収能が十分な衝突エネルギー吸収性能を持つかについて検討を行う。
▷ 応用可積分系(3) ［3月5日：13:30-14:50：C］（座長：間田 潤（日本大学））
- 土谷感染モデルの拡張について / ○南 凜歩 (早稲田大学基幹理工学部), 高橋 大輔 (早稲田大学基幹理工学部) [概要]
新型コロナウイルス感染症に関して土谷隆氏による離散数理モデルが報告されている．このモデルはSIRモデルの時間変数を離散化し，一定期間後の治癒の効果を考慮している．この土谷感染モデルでは，実効再生産数に関連する感染力の係数βが重要な役割を果たす．本講演では，このβを感染者数制御のための指標と捉え，入院患者数や経済指標にもとづく最適なβのコントロールを計算する拡張モデルについて述べる．
- SIRモデルの解構造を保存する離散化と厳密解 / ○丸野 健一 (早稲田大学理工学術院), 田中 悠太 (早稲田大学理工学研究科) [概要]
感染症の数理モデルとして知られているSIRモデルは2014年にHarkoらによって厳密解が求められている．この厳密解に着目しSIRモデルの解構造を保存する離散化を行い，得られた差分方程式に対して厳密解，保存量を構成する．また，得られた差分方程式を用いた数値計算例を示す．
- 多ソリトン解を持つ遅延可積分系 / ○中田 健太 (早稲田大学基幹理工学部), 丸野 健一 (早稲田大学理工学術院) [概要]
本講演では, 離散KP方程式と離散2次元戸田方程式に対してある操作を行うことで, 多ソリトン解を持つ遅延微分方程式が得られることを示す. また, 提案手法により, 戸田格子・Lotka-Volterraなどのいくつかのソリトン方程式を「遅延化」できることを述べる.
- 連続および離散弾性曲線の等周変形の明示公式とmKdV階層のテータ函数解 / ○重富 尚太 (九州大学大学院数理学府), 梶原 健司 (九州大学マス・フォア・インダストリ研究所) [概要]
オイラーの弾性曲線は、平面上の一次元弾性体を曲げたときの形状を表す曲線として知られている。
また、mKdV方程式の進行波解が弾性曲線の曲率が満たす微分方程式の解になっていることも知られている。
この事実に基づき、弾性曲線の可積分な離散化が定式化されてきた。本講演では、楕円テータ函数を用いた
弾性曲線の等周変形および離散弾性曲線の連続的・離散的等周変形の明示公式を提示する。
▷ 幾何学的形状生成 (3) ［3月5日：13:30-14:50：D］（座長：梅原 雅顕（東京工業大学））
- 逆さ吊りシミュレーションによる軸力抵抗型の形態創生 / ○田川 浩之 (武庫川女子大学建築学部), 竹内 莉乃 (武庫川女子大学建築学部) [概要]
建築家のガウディやフライ・オットーは、逆さ吊り模型を用いた物理的な実験を用いて、軸力抵抗型の形態を得て、サグラダ・ファミリアや樹木構造などを設計した。本研究では、非線形有限要素に基づく逆さ吊りシミュレーションにより、軸力抵抗型の樹木構造や積層ドーム構造の形態創生を試みる。具体的には、軸力のみ伝達するロッド要素で構成される不安定な構造モデルに対し、仮想的な減衰を与え、重力加速度下で、動的な逆さ吊りシミュレーションを行い、軸力のみでの釣合い形状を得る。
- 幾何学的変分問題による膜構造の形状決定法 / ○野涯 海斗 (鹿児島大学), 横須賀 洋平 (鹿児島大学), 本間 俊雄 (鹿児島大学) [概要]
本稿では、応力一定・応力密度一定とした幾何学的変分問題による膜・ケーブル・アーチ梁を用いた骨組膜構造の形状決定手法を提案する。
膜構造の初期形状は、張力を導入することが可能な初期曲面形状を得ることが必要となる。
エネルギ汎関数の定式化と数値解析結果を示し、解形状に対する応力変形解析を実施することで本手法の妥当性を示す。
- On the bifurcation and stability for surfaces with constant mean curvature bounded by two coaxial circles / ○奥田 健斗 (九州大学大学院数理学府), 小磯 深幸 (九州大学マス・フォア・インダストリ研究所) [概要]
平均曲率一定曲面（ＣＭＣ曲面）は「囲む体積を保つ変分に対する面積の臨界点」であり，シャボン膜や微小液滴の数理モデルとして知られている．ＣＭＣ曲面の解が安定か否か（面積極小か否か）の判定は重要課題であるが，一般には難解である．本講演では，回転軸を共有する２つの同じサイズの円で張られるＣＭＣ曲面に対して，楕円積分を用いた複雑な計算や分岐理論を応用して「既知の安定解に近い解」についての安定・不安定の判定を完成させたことを報告する．
- 楔型領域内の非等方的capillary超曲面の安定性 / ○岡 元基 (九州大学大学院数理学府) [概要]
近年, 非等方的エネルギーを用いた曲面の安定性に関する研究が行われている. 非等方的エネルギーは曲面の面積を一般化したエネルギーであり, 結晶に対するエネルギーとして, 数学以外の分野でも重要なエネルギーである. 本研究では楔型領域内にあり, 楔の辺と共通部分を持つ安定なcapillary曲面がWulff図形と相似な図形に限ることを示した. 今回は非等方的エネルギーの基本的事項と今回示した定理の証明の概要を紹介する.
▷ 数論アルゴリズムとその応用(1) ［3月5日：13:30-14:50：E］（座長：横山 俊一（東京都立大学））
- 2次強Frobeniusテストとその判定効率について / ○伊丹 洸陽 (東京都立大学大学院 修士課程2年), 篠原 直行 (情報通信研究機構 研究マネージャー), 内山 成憲 (東京都立大学教授) [概要]
確率的素数判定テストとして,一般的によく用いられているMiller-Rabinテストや,
Miller-Rabinテストよりも誤り率の小さい2次強Frobeniusテストがある.
この2つの素数判定テストを組み合わせ,パラメータを小さい素数から順に動かしたときに,
連続してテストを通過する最小の合成数を探索する研究が行われている.
この先行研究を受け,今回2次強Frobeniusテストのみを用いて同様の実験を行い,
5*10^11までの奇合成数において,x^2-x+2,x^2-x+3,及びx^2-x+5の3つに関して
2次強Frobenius擬素数となるものは存在しないことが分かった.
本発表では,先行研究の素数判定テストとの判定効率の比較や,実験結果に関する考察を述べる.
- F4アルゴリズムにおける多項式選択について / ○星 雄大 (東京都立大学大学院修士課程2年), 伊藤 琢真 (情報通信研究機構 研究員), 篠原 直行 (情報通信研究機構 研究マネージャー), 内山 成憲 (東京都立大学教授) [概要]
グレブナー基底を効率的に計算する代表的なアルゴリズムとしてF4アルゴリズムが挙げられる。F4アルゴリズムに限らず、グレブナー基底を計算するアルゴリズムの効率は、使用する項順序やS項式の選択、多項式の計算順序などに関係することが知られている。本発表では、多変数公開鍵暗号の暗号方式で利用される種類の多項式集合に注目し、F4アルゴリズムを用いて、そのグレブナー基底の計算における多項式の計算順序の考察について述べる。
- Signatureを用いたアルゴリズムによるMQ問題の計算 / ○坂田 康亮 (東京大学) [概要]
Signatureを用いたグレブナ基底を求めるアルゴリズムは、2001年に J.-C. Faugèreが提案したF5アルゴリズムを起源としており、これまでのアルゴリズムと比べて無駄な計算(zero reduction)を多く省くことが可能なアルゴリズムとして知られている。今回、連立二次変数代数方程式の解を求める問題（MQ問題）を対象とし、signatureを用いたアルゴリズムの有効性を考察した。
- Hufu-UOVの安全性について / ○橋本 康史 (琉球大学) [概要]
有限体上の多変数二次多項式の集合を公開鍵としてもつ署名方式の一つであるUOVは、適切にパラメータを選ぶことで十分な安全性を確保できるとともに、署名認証・生成を効率的に行うことができると考えられている。その一方で、鍵のサイズが比較的大きくなりがちであることから、鍵のサイズを小さくする取り組みが行われてきている。Hufu-UOVはそのような小さい鍵をもつUOVのひとつで、Circulant行列やToeplitz行列を利用して鍵サイズの圧縮に成功している。ただし、このような「特殊な」構造を導入することで脆弱性が
生じた例は枚挙にいとまがない。本講演では、Hufu-UOVの特殊な構造によってどの程度
安全性が損なわれたかを説明する。
▷ 数理ファイナンス(3) ［3月5日：13:30-14:50：F］（座長：中津 智則（芝浦工業大学））
- 時間非一様なMarkov過程の効率的サンプルパス生成とバリア・ オプションのGreeks計算 / ○石谷 謙介 (東京都立大学) [概要]
講演では，停止時刻を含むようなWiener汎関数に対する超関数微分の計算方法と，その応用としてバリア・オプションのGreeksの準解析的計算方法を提案する．更に，この提案手法を用いてGreeksを計算するために必要となる，3次元Bessel橋，Brownian meanderやBrown引越過程といった時間非一様なMarkov過程の効率的サンプルパス生成方法についても紹介し，提案手法を用いてバリア・オプションのGreeksを高精度に計算できることを確認する．
- Non-Gaussian強度をもつ多変数ホークス過程のExact Simulation / ○吉田 賢樹 (法政大学理工学研究科), 安田 和弘 (法政大学) [概要]
Qu et al.(2019)はNon-Gaussian強度をもつホークス過程を構築し，そのExact Simulationを与えている．本講演では，Non-Gaussian強度をもつホークス過程を多次元化した，Non-Gaussian強度をもつ多変数ホークス過程を導入し，そのExact Simulationを与える．また，数値例において理論値とシミュレーション値を比較し，構築したアルゴリズムの妥当性を検証する．Non-Gaussian強度をもつ多変数ホークス過程は，ファイナンスや保険，その他の分野に存在する伝播リスクのモデリングに対して有用な特徴をもっている．
- Tanaka-Yor 方程式を用いた確率微分方程式の解の存在判定 / ○田村 勇真 (立命館大学大学院) [概要]
Yor 方程式は非正整数を添え字とする離散確率過程であったが，本講演では特別な形の Yor 方程式を Tanaka-Yor 方程式と名付け，その解を観察することによって非負実数を添え字とする確率微分方程式に対して「弱解は存在するが強解は存在しないための十分条件」を与える．
- The Thermodynamic Approach to Whole-Life Insurance: A Method for Evaluation of Surrender Risk / ○井田 有紀 (立命館大学) [概要]
In the presentation, we introduce a collective model, hinted by statistical mechanics, for life insurance
where the heterogeneity, including health state, of each insured is modeled by a diffusion process.
Using the proposed framework, one can describe the total pay-off as a functional of the diffusion process,
which can be used to derive a level premium that evaluates
the risk of the lapses due to the so-called adverse selection.
Two numerically tractable models are presented to exemplify the flexibility of the proposed framework.
▷ 科学技術計算と数値解析(3) ［3月5日：15:00-16:20：A］（座長：降籏 大介（大阪大学））
- 最悪誤差の勾配近似によるkernel herdingアルゴリズムの加速 / ○辻 和真 (東京大学大学院情報理工学系研究科), 田中 健一郎 (東京大学大学院情報理工学系研究科、JSTさきがけ) [概要]
kernel herdingとはRKHS上で制約付き最適化問題を解くことで数値積分公式を構成する手法である。この手法で構成される数値積分公式は数値的安定性を持つなど良い性質を持つ一方、積分誤差の収束が他手法と比較して遅いという問題点がある。本研究では最悪積分誤差の勾配方向の近似を部分問題として解く手法を提案し、収束速度の改善を行う。講演では提案手法の理論解析および数値実験結果について説明をする。
- 佐藤超函数論に基づく補間、数値微分、および数値不定積分 / ○緒方 秀教 (電気通信大学) [概要]
本講演では、既存の数値積分公式（ガウス型公式、DE公式、IMT型公式など）を用いて、佐藤超函数論に基づく関数補間、数値微分、および数値不定積分を行う方法を提案する。本方法では、補間等を行う関数に対し、それを佐藤超函数と見なしたときそれを与える「標準定義関数」とよばれる複素解析関数を数値積分により計算して、実軸上に解析接続することにより補間、数値微分、数値不定積分を行う。
- 幻影解が共存する陰的システムにおけるランダムネス付加の影響について / ○畑上 到 (東京都市大学共通教育部) [概要]
複数の安定解が共存する場合の非線型偏微分方程式系における複雑な数値解構造へのランダムなノイズが及ぼす効果について，数値実験により考察した．グレイースコット方程式を陰解法で解く場合をモデルとして，幻影解が存在する離散パラメータ領域におけるノイズ付加による安定化，ランダムネスの大きさの初期値依存性への影響等について考察した．
- グラフ求積へのFrank–Wolfe法の適用 / ○大城 隆之介 (東京大学大学院情報理工学系研究科), 田中 健一郎 (東京大学大学院情報理工学系研究科) [概要]
近年データサイエンスへの応用の点からグラフ上の求積が注目されている．
本発表では Frank–Wolfe 法とその派生によるグラフ上の求積公式を設計を提案する．これらの手法は再生核 Hilbert 空間上の求積公式の設計法として考えられていたが，これをグラフ上の関数へ適用することを考える．
本手法は理論評価が得られる．数値実験より本手法はグラフ上の求積公式の設計手法として有効であることが観察される．
▷ 折紙工学(3) ［3月5日：15:00-16:20：B］（座長：斉藤 一哉（九州大学））
- A comparison of different folding models in valid overlapping order problems / ○Jia Yiyang (筑波大学), Mitani Jun (筑波大学), Uehara Ryuhei (北陸先端科学技術大学院大学) [概要]
We compared the capability of three folding models: general folding model, some-layers simple folding model, and some-layers simple folding-unfolding model in three distinct valid overlapping order problems: the valid total overlapping order problem of 1×n maps(1D VOP), the valid total overlapping order problem of m×n maps(Total VOP), and the valid boundary overlapping order problem of m×n maps(Boundary VOP). We show that even though the three models appear with the same reachability of the overlapping order in 1D VOP, their reachable valid overlapping orders in both Total VOP and Boundary VOP are in strict inclusion relations.
- 三角形メッシュモデルを対象とした簡易折りあげ可能な展開図の生成 / ○加藤 優弥 (筑波大学), 三谷 純 (筑波大学) [概要]
メッシュモデルの展開図を生成するソフトウェアの一つにOrigamizerが挙げられる。
しかし、生成される展開図は折線数が多く、折るのに多大な苦労を要する。
本発表では、素材によっては多少のズレなら許容できることを基に、一部の折線を除去して展開図を簡略化する手法を提案する。
また、折線の除去をよりしやすくすることを目的として、エッジコラプスを用いてメッシュモデルの簡略化を行う。
- ホール問題における局所的に平坦折り可能な展開図を用いた平織りの作成手法 / ○中里 陸 (筑波大学), 山本 陽平 (筑波大学), 三谷 純 (筑波大学) [概要]
折り紙設計におけるホール問題とは、展開図上で折り線の配置が定まっていない領域に適切な折り線の配置を求める問題である。この解を生成するアルゴリズムは既に知られているが、平坦折り可能であることが保証されていない。そこで本研究では、局所的に平坦折り可能な山谷割り当てを持つ展開図を出力する機能を追加し、平織りと呼ばれる折り紙の技法に適用する手法を考案した。また、応用例としてプリーツが特定の角度で交差する領域に適した展開図を作成した。
- 正四面体の表面の折りたたみと四次元折り紙 / ○奈良 知惠 (明治大学) [概要]
三次元空間にある正四面体の表面について，隣接する二面を共有辺の周りに回転させ，これら二面の間にある他の二面に対して「ひし形の翼折り」による移動折り目を用いると，正四面体を切ったり伸ばしたりせずに平坦化できる。一方，この正四面体が四次元空間にあるときには，「四次元の折り紙」を使うと，別つの方法によって移動折り目を用いなくても平坦化できる。ここでは，これら二つの方法に注目しながら，四次元の正軸体の二次元スケルトンを連続的に平坦化するときの面の重ね順について報告する。
▷ 応用可積分系(4) ［3月5日：15:00-16:20：C］（座長：丸野 健一（早稲田大学））
- フーリエ補間法によるハミルトン系の時間発展 / ○佐々 成正 (日本原子力研究開発機構) [概要]
これまで, シンプレクティック数値積分法が
相空間の面積和を保存するスキームである事
について議論を行ってきた. その際, フーリ
エ補間法が, 補間点の時間発展を十分な精度
で再現できるとの前提条件の下で理論を構成
している. 本稿では, フーリエ補間法による
ハミルトン系の時間発展問題において, その
計算精度等について詳しく吟味したい.
- 完全グラフに対応する離散ソボレフ不等式の最良定数の発展 / ○山岸 弘幸 (都立高専) [概要]
完全グラフに対応する離散ソボレフ不等式の最良定数を求めた。さらにその発展として、完全二部グラフへの適用や、離散Lpソボレフ不等式への拡張を試みた。
- Discretization of integrable sub-cases of the Hénon-Heiles system and the Lorenz system / ○飯野 寛大 (東京大学大学院数理科学研究科), Willox Ralph (東京大学大学院数理科学研究科) [概要]
本講演では，Hénon-Heiles系とLorenz系の可積分な場合の離散化を行う．具体的には，考察する条件下で両系が楕円関数解を持つという性質に着目し， QRT写像を導く離散スキームを両系に適用する．また，Lorenz系に対しては，広田の離散化を行うことでもう１つの離散系を導出する．最終的に，得られる３つの双有理写像は，次数増大が多項式オーダーになるだけでなく，離散Liouville可積分性を持つことが判明する．
- 血管新生の数理モデル ー３次元への拡張ー / ○酒井 一馬 (東京大学大学院数理科学研究科), 林 達也 (北海道大学大学院情報科学研究院), 間田 潤 (日本大学生産工学部), 時弘 哲治 (東京大学大学院数理科学研究科), 礪波 一夫 (東京大学大学院医学系研究科), 栗原 裕基 (東京大学大学院医学系研究科) [概要]
血管新生とは，既存の血管から新しい血管が構築される現象である．我々は血管内皮細胞を質点ではなく楕円体粒子と仮定し，血管新生を記述する離散数理モデルを構築した．楕円体の形状を変化させることで，形成されるパターンに違いが見られた．本講演では，３次元に拡張した数理モデルを紹介し，数値シミュレーション結果について検討する．
▷ 幾何学的形状生成 (4) ［3月5日：15:00-16:20：D］（座長：三浦 憲二郎（静岡大学））
- 対数型美的曲線の空間曲線・曲面への拡張 / Schief Wolfgang (ニューサウスウェールズ大学), 梶原 健司 (九州大学), ○軸丸 芳揮 (九州大学) [概要]
日本刀の形状などに現れる「美しい曲線形状」は，対数型美的曲線と呼ばれる曲線のクラスを与える．
平面弾性曲線が曲線の非伸縮変形に対する可積分条件の進行波解として現れる一方，対数型美的曲線は曲線の「等角度変形」に対する可積分条件の進行波解とみなすことができる．
この意味において，対数型美的曲線は弾性曲線の相似幾何類似である．
本講演では空間曲線に対して曲線の等角度変形を考察し，システムの擬球型曲面との対応や具体例について紹介する．
- Bonnet族の極小曲面における曲率線の一般式 / ○鈴木 利友 (武庫川女子大学), 緒方 勇太 (沖縄工業高等専門学校) [概要]
曲率線が平面曲線となる極小曲面は、平面、懸垂面、Enneper曲面、およびBonnet族の極小曲面（以下Bonnet曲面とする）に限られることが既に知られている。このうちBonnet曲面の曲率線は、パラメータに三角関数を含む楕円Duporcq曲線、双曲線関数を含む双曲線Duporcq曲線および懸垂曲線からなることを示した。なおBonnet曲面は周期性があるが、周期を0とおくと楕円Duporcq曲線は円、双曲線Duporcq曲線は懸垂曲線に変化し、懸垂面と一致する。
- ［企画講演：40分］ 数学をベースとする技術を使うソフトウェア開発現場から見えること / ○宮崎 祐樹 (株式会社アルモニコス) [概要]
株式会社アルモニコスは、数学をベースとする3次元形状処理技術をコアコンピタンスとして、 お客様の課題を解決するソフトウェアを開発・ご提供しています。
本講演ではソフトウェア開発の現場から、
・製造業の現場で求められる数学的テーマ
・数学研究を活用する側の視点
・具体的な産学連携の事例
・数学科出身者から見る、業務に活かされる数学知識と経験
上記4点についてご紹介します。
▷ 数論アルゴリズムとその応用(2) ［3月5日：15:00-16:20：E］（座長：谷口 哲也（金沢工業大学））
- Modular Magic Sudoku の構成 / ○足立 智子 (東邦大学), 桑嶋 大地 (東邦大学) [概要]
Modular Magic Sudokuは、数独に条件「各小方陣において、行和、列和、対角線和が法n^2で0と合同」を加えたものである。
位数が最小の9の場合には、Lorch and Weld (2012)により、その構造が解明されている。
そこで、本発表では、ある条件を満たす一つの小方陣からModular Magic Sudokuを構成する方法を提案する。
- より広範囲のナップザック暗号の解読可能性と組合せ論的整数論の視点 / ○鎌田 祥一 (東京都立大学) [概要]
ナップザック暗号は部分和問題や部分積問題などのナップザック問題の求解困難性を安全性の根拠を置いている公開鍵暗号（暗号方式／署名方式）の総称である．これらのナップザック問題は組合せ論的整数論における問題であると同時にNP困難な問題でもある．多くのナップザック暗号は部分和問題の特徴を利用した低密度攻撃と呼ばれる攻撃法により解読が可能である．解読方法が未知の数少ない暗号方式としてOkamoto-Tanaka-Uchiyama (OTU)暗号 (2000) が知られている．本講演では，等差数列についての Szemer\\'{e}di の定理を真似た言明として Szemer\\'{e}di 型仮定を導入し，平均的な場合と最悪の場合の求解困難性はどのように解釈すべきかをまず述べる．次に，平均的な場合の低密度攻撃における直交格子の最小ノルムの分布についての実験結果から，低密度攻撃の失敗に必要な密度が先行研究の理論的結果よりも広いことを示す．最後に，展望としてOTU暗号の安全性評価を厳密に行うためには何が必要になりそうかについて，組合せ論的整数論の視点から述べる．
▷ ウェーブレット ［3月5日：15:00-16:20：F］（座長：萬代 武史（大阪電気通信大学）、鈴木 俊夫（東京理科大学））
- Haarウェーブレットを用いたディストーションサウンドの解析手法の改良 / ○石田 大河 (東京理科大学大学院理学研究科応用数学専攻), 鈴木 俊夫 (東京理科大学理学部第一部応用数学科), 石渡 恵美子 (東京理科大学理学部第一部応用数学科) [概要]
エレキギターなどのディストーションサウンドを用いた楽器音は非可逆変換を含むフィルタを用いて構成されるため，Fourier変換を用いた解析は難しいとされている．本研究では，先行研究で報告されているウェーブレット変換を用いた特徴量の改良を行った．Haar ウェーブレットのパラメータを適切に定めることにより，特徴量を差分法で近似的に表すことが可能となり，計算時間を短縮できることがわかった．
- Mellin 変換を用いた音声信号のスケールパラメータの推定 / ○守本 晃 (大阪教育大学) [概要]
スケール不変な Mellin 変換を用いて，音声信号がスケール変換の関係にあるかないかを調べる方法を提案する．スケール変換の関係にある場合は，スケールパラメータを推定する．録音した音声信号を用いて，提案したアルゴリズムの検証を行う．
- Uncertainty Principles Related to Fractional Fourier Transform / Bahri Mawardi (Department of Mathematics, Hasanuddin University), ○Ashino Ryuichi (Mathematics and Informatics, Osaka Kyoiku University) [概要]
A direct relation between the Fourier transform and the fractional Fourier transform is studied.
Some properties of the fractional Fourier transform are investigated using this relation.
Several versions of uncertainty principles involving the fractional Fourier transform are presented.
- 平均律半音階ウェーブレットに関する考察 / ○戸田 浩 [概要]
無理数ダイレーションを持つ正規直交ウェーブレット基底や，そのHilbert変換ペアの存在は証明されており，これらを基礎に平均律半音階ウェーブレットの設計は可能である．しかし実用化にあたっては，構造の複雑さや，計算の難しさ等の問題が存在する．今回はそれらを考察する．
▷ 科学技術計算と数値解析(4) ［3月5日：16:30-17:50：A］（座長：剱持 智哉（名古屋大学））
- 動的境界条件下のCahn-Hilliard方程式に対する離散変分導関数法スキームの多段線形化とその解析 / ○奥村 真善美 (大阪大学 大学院情報科学研究科) [概要]
未知関数の時間微分をその条件内に含む動的境界条件下のCahn-Hilliard方程式系に対する線形の構造保存スキームを提案する．非線形問題に対する通常の離散変分導関数法スキームは非線形となり，計算コストが高いという欠点があるが，本研究では，スキームの線形化手法の多段階線形化を用い，線形の離散変分導関数法スキームを構成した．本講演では構成したスキームを紹介するとともに，そのスキームの安定性，可解性の結果および数値実験結果について述べる．
- Ostrovsky方程式の構造保存スキームの数学的解析 / ○川合 秀人 (東京大学工学部計数工学科), 佐藤 峻 (東京大学大学院情報理工学系研究科), 松尾 宇泰 (東京大学大学院情報理工学系研究科) [概要]
Ostrovsky方程式とは，u_{tx} = f(u,u_x,…)の形の偏微分方程式の中でも数値計算スキームの研究がそれほど進んでいない，(u_t+h_x(u,u_x,…))_x = u型の偏微分方程式である．この方程式の数値計算スキームとしては，真の解が持つ大域的性質の一部を離散化後にも保存するように構成されたもの（T. Yaguchi et al., 2010）があり，実際にその有用性が数値実験で示されてはいるが，数学的な解析はまだ行われていない．
本研究では，Ostrovsky方程式の構造保存な数値計算スキームに対する数学的な解析を行い，その可解性と収束性を示した．特に収束性について，似た形のmHS方程式に対する先行研究（S. Sato, 2019）が対象の特殊性に基づいて証明を行っていたのに対し，より一般的な方程式にも適用できる可能性のある論理展開での証明を行った．
- ウィルモア流方程式に対する構造保存数値解法の構築 / ○宮﨑 瑛士 (名古屋大学物理工学科), 剱持 智哉 (名古屋大学大学院工学研究科), 曽我部 知広 (名古屋大学大学院工学研究科), 張 紹良 (名古屋大学大学院工学研究科) [概要]
本発表では、閉曲線に対するウィルモア流方程式の数値計算手法を提案する。本手法では、折れ線によって曲線を離散化し、離散変分導関数法を用いて法線速度の離散化を行う。また、頂点の集中を防ぐため、デッケルニックによる接線速度を導入する。ただし、接線速度の導入過程で、修正項を追加する。この修正項により、提案スキームは頂点の集中を防ぎつつ、エネルギー散逸性を保つことができる。発表の最後に数値計算例をいくつか紹介する。
- Scalar Auxiliary Variable法と保存的exponential Runge-Kutta法の組合せによる高速かつ高精度なスキームの構成 / ○佐藤 峻 (東京大学大学院情報理工学系研究科) [概要]
本講演では，ある仮定を満たす保存的な発展方程式に対して，Scalar Auxiliary Variable法と保存的exponential Runge-Kutta法を組み合わせることで，高精度で高速な保存的数値解法を構成する．特に提案手法の計算コストの主要部は元の問題のサイズの行列指数関数の計算であり，陽的なexponential Runge-Kutta法とほとんど同程度となる．
▷ 折紙工学(4) ［3月5日：16:30-17:50：B］（座長：舘 知宏（東京大学））
- 新型コロナ肺炎を折り紙モデルで理解する / ○北岡 裕子 (東京農工大学) [概要]
新型コロナ肺炎はウイルスがⅡ型肺胞上皮細胞に感染することで生じる。重篤な呼吸不全に至るのは、Ⅱ型肺胞上皮細胞が産生分泌する肺サーファクタントが欠乏することによって肺胞が虚脱するからであるが、複雑な4次元構造体である肺胞系の動態とその異常を理解するのは容易ではなく、現在の医学界では正しく理解されていない。演者は折り紙肺胞モデルを作成し、ウイルス感染による肺胞構造の変化をシミュレートした。
- CSG（constructive solid geometry）技術援用複雑ハニカム構造の高精度高効率生成法 / ○ディアゴ ルイス (明治大学), 篠田 淳一 (明治大学), 萩原 一郎 (明治大学) [概要]
切り紙・折り紙は今や折紙工学の一大トピックである。その構造はハニカム構造となる。これまで非凸の曲面形状のコアの展開図が困難で、例えば車両の内装材くらいの複雑形状となると一続きの展開図を得ることは困難であり、構造をいくつかに分割しそれぞれの展開図をつなぐという方式で検討されていた。今回、複雑構造でも一続きのハニカム構造が得られることとなり強度剛性はじめ関連特性の飛躍的な向上が期待される。
- 斜角型ハニカムコアの開発とその視覚効果 / ○斉藤 一哉 (九州大学), 岩元 真明 (九州大学), 中元 翔一 (九州大学) [概要]
周期的なスリットを入れたシートを折り曲げて立体化させることでハニカム構造を製造する折紙工法を応用して、
6角柱のセルがパネル面に対し傾斜した特殊な斜角型ハニカム構造を開発した。
本講演では斜角型ハニカムコアの展開図設計法やその特殊な視覚効果について解説する。
- 配列の異なるコアパネルの幾何学形状と機械的特性の関係 / ○岡安 晃平 (明治大学), 石田 祥子 (明治大学) [概要]
コアパネルは軽量で高強度，高剛性の特徴を持つ板状部材であり，建築や輸送機器などに広く用いられている．一般的にコアパネルの形状は，基本となる多面体コアを規則的に配置することで設計される．本講演では，空間充填可能な切頂八面体を異なる向きに配列して設計した4種類のコアパネルにおいて，配列の違いが強度，剛性といった機械的特性に与える影響について，有限要素法による解析結果を報告する．
